Dviejų kamerų tarpusavio padėties įtaka trimačių vaizdų rekonstrukcijai

Įvadas

Stereoskopijoje trimačiai vaizdai rekonstruojami atsižvelgiant į žmogaus akių fiziologines savybes – regos disparatiškumą [1] ir siekiant gauti kuo tikroviškesnį vaizdą. Aplinkos analizei taikomos trimačių vaizdų rekonstrukcijos tikslas yra priešingas – kiek įmanoma tikslesnė aplinkoje esančių objektų trimatė rekonstrukcija, kad juos būtų galima įvertinti ar atpažinti. Šio tipo trimatės rekonstrukcijos taikymo sritys yra įvairios. Iš jų galima būtų išskirti nedestruktyviąją medžiagotyrą, mechatroniką, mediciną. Būtent šioje plotmėje toliau pažvelgiami atlikto darbo rezultatai.

Rekonstruojant trimačius vaizdus, reikia įvertinti daugybę įvairiausių parametrų. Tokie parametrai kaip kameros židinio nuotolis, jutiklių matricos skyra, apžvalgos kampas ir pan. dažnai laikomi nekintamais. Tuo tarpu kiti parametrai: kampas ir atstumas tarp kamerų, atstumas nuo kameros iki rekonstruojamo objekto, vaizdų sutapdinimo klaidos ir pan., gali keistis. Pastaruosius rekonstrukcijos parametrus galima sąlygiškai išskirti į dvi rūšis: valdomus (kampas ir atstumas tarp dviejų kamerų, atstumas nuo kameros iki objekto ir t. t.) ir nevaldomus (kamerų judėjimas, būdingųjų taškų paieškos ir sutapdinimo klaidos ir t. t.). Toliau bus analizuojama nevaldomų parametrų įtaka rekonstrukcijai, kai yra keičiamas kampas tarp dviejų kamerų.

Rekonstrukcijai naudojant dvi kameras, visų pirma reikia nuspręsti, kaip jos bus išdėstytos viena kitos atžvilgiu, – parinkti kampą tarp jų. Idealiu atveju, kai nėra kamerų kalibravimo ir taškų koordinačių nustatymo netikslumų ir nejuda nei objektas, nei kamera, galima nustatyti kiekvieno taško, matomo abiem kameromis, padėtį erdvėje. Realiai susiduriama su nepakankamai tiksliu kamerų kalibravimu, iškraipymais, kuriuos lemia būdingųjų taškų paieškos ir vienas kitą atitinkančių taškų paieškos sistemos, kvantavimo iškraipymai ir kamerų vibracija. Nepageidaujamas kamerų vibravimas ir tokio pobūdžio triukšmų įtakos mažinimas literatūroje retai minimi, todėl toliau tam bus skirta nemažai dėmesio.

Kamerų išdėstymas taip pat lemia svarbų trimatei vaizdų rekonstrukcijai parametrą – minimalų pastebimą paviršiaus pokytį. Jis priklauso nuo kameros vidinių parametrų ir atstumo nuo kameros iki analizuojamo objekto. Taigi atsižvelgiant į kameros parametrus, reikia parinkti tokį kamerų išdėstymą, kad analizuojamo paviršiaus trimatė rekonstrukcija būtų atlikta kuo tiksliau.

Kameros vibravimo įtaka vaizdo tikslumui

Vibruojant kamerai atsiranda iškraipymų, kuriuos galima vertinti kaip netikslų taško koordinačių nustatymą kamera gautame vaizde. Žinant kameros polinkio kampą δ ir remiantis [2], tikslus sąryšis tarp taško koordinačių x, y, z erdvėje ir taško koordinačių x_δ , y_δ kameros plokštumoje išreiškiamas lygtimis:

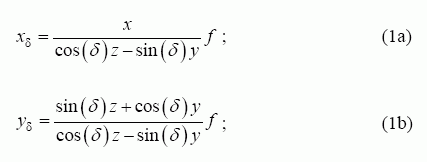
čia f – kameros židinio nuotolis. Savo ruožtu kameros vibravimas gali būti aprašytas nurodant kameros pasukimus apie vieną iš trijų koordinačių ašių ir kameros poslinkį – koordinačių pradžios taško judėjimą. Sakykime, kad kameros koordinačių pradžios taškas nejuda ir iškraipymus lemia tik kameros pasukimai apie x, y, z ašis. Taip gaunamos atitinkamai ε_x , ε_y , ε_z taško koordinačių klaidų dedamosios. Norint jas įvertinti, (1) išraišką galima apibendrinti taip:

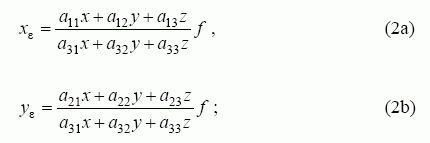
čia a koeficientai sudaro objekto vaizdo transformacijos į kameros koordinačių sistemą A matricą; x_ε ir y_ε yra taško koordinatės, gautos įvertinant kameros vibraciją.

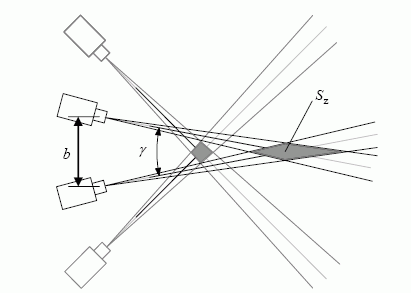
1 pav. Neapibrėžtumo sritis, gaunama dėl kamerų judėjimo

Koeficientai a gali būti išreikšti kameros polinkio kampu δ ir iškraipymų dedamosiomis ε_x , ε_y , ε_z :

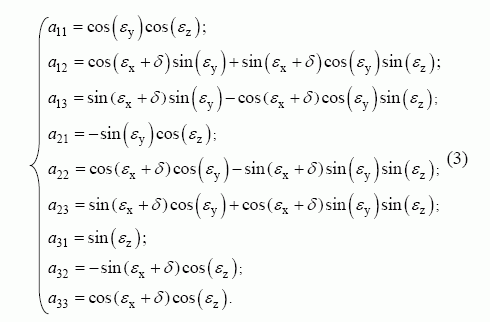
Sakykime, kad kamera vibruoja tik z ašyje. Kadangi šiuo atveju paskutinėje išraiškoje yra tik viena klaidos dedamoji ε_z , pertvarkius (1) išraišką, gaunama:

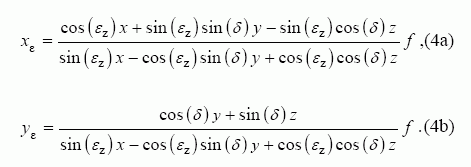
Kaip matyti iš šių išraiškų, kameros judėjimas apie z ašį turi įtakos taško koordinačių nustatymo tikslumui ir kitose ašyse – x ir y . Į tai būtina atsižvelgti kuriant ir diegiant trimačių vaizdų rekonstrukcijos sistemas.

Neapibrėžtumo sritį veikiantys veiksniai

Esant iškraipymų dėl nepageidaujamo kamerų sukimosi apie z ašį trimačių vaizdų rekonstrukcijos sistemoje, sudarytoje iš dviejų kamerų, atsiranda neapibrėžtumo – kameros jutiklių neregistruojama – sritis (1 pav.). Šios srities plotas Sz priklauso nuo b atstumo tarp kamerų bei nuo γ kampo tarp jų [3].

Žinant priklausomybes tarp neapibrėžtumo srities, gaunamos judant kameroms bei keičiantis atstumui ir kampui tarp kamerų, galima būtų parinkti tokį kamerų išsidėstymą, kad neapibrėžtumo sritis neviršytų norimos ribos. Iš 2 pav. pateiktų modeliavimo rezultatų matyti, kad, mažinant atstumą arba kampą tarp dviejų kamerų, galima sumažinti neapibrėžtumo sritį – kameros sukimosi apie z ašį įtaką trimačių vaizdų rekonstrukcijai.

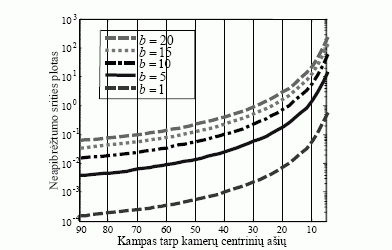
2 pav. Neapibrėžtumo srities ploto charakteristikos

Trimačių vaizdų rekonstrukcijoje taip pat reikia įvertinti rekonstruojamo objekto paviršiaus struktūrą ir aplinkos įtaką (objekto apšvietimą, įvairius atspindžius ir pan.). Aplinkos įtaka kameroms vienodėja, kameras išdėstant lygiagrečiai bei artinant vieną prie kitos.

Mažiausią pastebimą pokytį veikiantys veiksniai

Kameros apžvalgos laukas nurodo taškus, kurie yra matomi kameroje . Apžvalgos stereolaukas nurodo tuos objekto taškus, kurie yra matomi abiejų kamerų. Reikia atkreipti dėmesį į tai, kad nepriklausomai nuo kameros lęšių, tik tam tikru atstumu nutolę objekto taškai bus ryškiai matomi. Visi kiti taškai bus daugiau ar mažiau susilieję.

Dviejų kamerų apžvalgos stereolaukas yra plačiai aprašytas [4]. Tarkime, kad analizuojami objektai yra nutolę nuo kameros tik du kartus didesniu atstumu nei kameros, nutolusios viena nuo kitos. Galima nesunkiai įsitikinti, kad sumažinus kampą tarp kamerų 30º , apžvalgos laukas padidėja 2,5 karto. Kartu sumažėja nepageidaujamo kamerų judėjimo įtaka.

Norint kuo tiksliau rekonstruoti trimačius vaizdus, reikia įvertinti mažiausius analizuojamo objekto paviršiaus pokyčius ir kiek įmanoma tiksliau išskirti būdinguosius taškus, kuriuos vėliau galima naudoti trimačių vaizdų rekonstrukcijai. Mažiausias pastebimas analizuojamo paviršiaus pokytis taip pat priklauso nuo minimalaus kampo pokyčio, kurį galima pastebėti [5]. Šis parametras taip pat priklauso ir nuo kameros jutiklio matricos skyros.

Mažiausias pastebimas pokytis D (3 pav.) gali būti išreikštas mažiausiu pastebimu kampo pokyčiu:

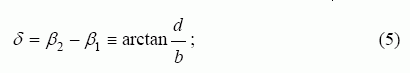
čia d – plotis srities, kurią dengia vienas jutiklis. Šis parametras gali būti apskaičiuotas pagal formulę

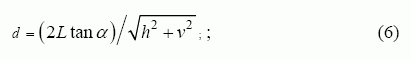
čia α – kameros apžvalgos kampas; h ir v – atitinkamai jutiklių skaičius kameros jutiklių matricos horizontalėje ir vertikalėje.

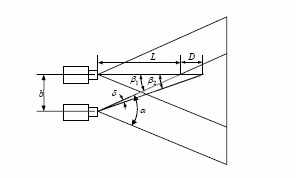
3 pav. Mažiausio pastebimo pokyčio iliustracija

Remiantis (5) ir (6) išraiškomis ir 3 pav. matyti, kad esant pastoviam h ir v mažiausias pastebimas pokytis mažėja, kai didinamas atstumas tarp kamerų arba mažinamas atstumas nuo kamerų iki objekto, arba mažinamas mažiausias pastebimo pokyčio kampas. Dar vienas būdas sumažinti dydį D – didinti γ kampą tarp kamerų centrinių ašių (1 pav.).

Objekto stebėjimo kampo įtaka būdingųjų taškų paieškai vaizde

Trimačių vaizdų rekonstrukcijoje dviejų kamerų vaizduose ieškoma būdingųjų taškų ir jų tarpusavio atitikmens ir tuo remiantis sprendžiama apie objekto ir jo paviršiaus struktūrą. Rekonstruojamo objekto tipas dažnai lemia būdingųjų taškų parinkimo algoritmą, pvz., veido būdingiems taškams išskirti naudojami vaizdu pagrįsti, požymiais pagrįsti ar kombinuoti metodai [6].

Tolesniuose tyrimuose taikytas Harris ir Stephens [7] pasiūlytas būdingųjų taškų paieškos algoritmas. Šis algoritmas remiasi vaizdų autokoreliacijos skaičiavimu. Prieš tai vaizdai dar filtruojami:

čia I – pradinis vaizdas; M – filtro kaukė; C – nufiltruotas vaizdas; x ir y atitinkamai nurodo apdorojamo vaizdo taško eilutės ir stulpelio numerį; i ir j – atitinkamai filtro kaukės stulpelių ir eilučių indeksai.

Vaizdui sulieti dažniausiai taikomos šios kaukės: diferencinė, centruota, paprastoji suliejimo, Gauso. Šiuose tyrimuose naudosime Gauso vaizdo suliejimo kaukę:

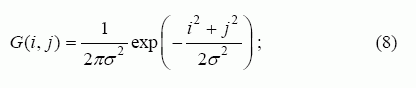
čia σ² – dispersija. Naudojantis šia kauke, vaizdas kraštuose suliejamas švelniai, o visi smulkūs elementai mažesni už pasirinktą kaukės dydį efektyviai pašalinami. Vaizdų spalvų suliejimas yra išsamiai aprašytas [8,9].

Vaizdo autokoreliacija gali būti išreikšta kaip atskirų taškų intensyvumų skirtumų kvadratų suma:

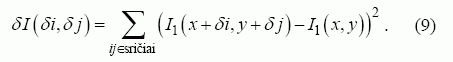
Eksperimentams naudotas Rubiko kubas, fotografuotas sukant jį apie vertikaliąją ašį kas 5º nuo 0º iki 90º. Gautuose vaizduose analizuota viena iš kubo plokštumų, ieškant būdingųjų taškų, nekeičiant filtro parametrų. Gauso filtro kaukės plotis parinktas lygus 9, remiantis bandymais su įvairaus pobūdžio vaizdais [10].

Dydis σ pariktas lygus 4, kadangi ši vertė bandymų metu lėmė didesnį rastų naudingų būdingųjų taškų skaičių. Parinktame būdingųjų taškų skaičiavimo algoritme galima nurodyti leistinų rasti būdingųjų taškų skaičių. Parinkę per didelį šį skaičių, galima gauti daug nepageidaujamų taškų (žr. 4 pav.). Nagrinėjamu atveju maksimalus leistinų rasti būdingųjų taškų skaičius 150 leido nustatyti daugiausiai naudingųjų taškų beveik visame stebėjimo kampų intervale, sukant kubą nuo 0º iki 60º.

4 pav. Būdingųjų taškų paieškos rezultatai esant maksimaliam leistinų rasti taškų skaičiui: a – 150; b – 350

Trimačių vaizdų rekonstrukcijoje reikia rasti kuo daugiau būdingųjų taškų, siekiant kuo tiksliau apibrėžti paviršiaus struktūrą. Būdingųjų taškų paieškos eksperimentų rezultatai yra pateikti 5 paveiksle.

Kai nustatytas maksimalus leistinų rasti būdingųjų taškų skaičius viršija 140–150, naudingų taškų skaičius labai kinta. Pavyzdžiui, jei parenkamas maksimalus taškų skaičius lygus 200, naudingų būdingųjų taškų skaičius kinta nuo 140 iki 200, objektą pasukus vos 5º kampu (5 pav.). Atliktų eksperimentų metu nustatyta, kad pagal pasirinktą algoritmą kubo vaizde randama ne daugiau kaip 210 naudingųjų būdingųjų taškų. Kaip matyti 5 paveiksle, kai leistinų rasti būdingųjų taškų skaičius yra artimas 150, randami tik naudingieji taškai stebėjimo kampui kintant nuo 0º iki 60º. Tai yra apie 70 % visų galimų rasti naudingų būdingųjų taškų.

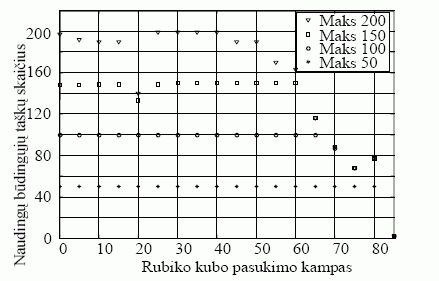
5 pav. Naudingų būdingųjų taškų paieškos rezultatai

Kitas trimačių vaizdų rekonstrukcijos etapas yra vienas kitą atitinkančių būdingųjų taškų paieška. Šiame etape kamerų tarpusavio padėtis taip pat yra vienas iš labai svarbių sutapdinimo tikslumą lemiančių veiksnių. Kadangi taškams sutapdinti naudojami koreliacija pagrįsti algoritmai, kampo tarp kamerų centrinių ašių padidinimas lemia nevienodas objekto paviršiaus apšvietimo sąlygas bei didelius perspektyvos kitimus. Todėl, naudojant koreliacija pagrįstus būdingųjų taškų sutapdinimo metodus, kameras rekomenduojama išdėstyti taip, kad kampas tarp centrinių ašių neviršytų 20º [11].

Išvados

Iškraipymus, gautus dėl nepageidautino kamerų judėjimo apie vertikaliąją ašį, galima sumažinti padidinus kampą tarp kamerų centrinių ašių.

Padidinus kampą tarp kamerų centrinių ašių, esant nedideliems atstumams iki objekto, stereolaukas padidėja. Trimačių vaizdų rekonstrukcijos tikslumas didėja didinant kampą tarp kamerų centrinių ašių ir mažinant atstumą iki objekto.

Keičiant kampą tarp kamerų nuo 0º iki 60º, keičiasi ir objekto stebėjimo kampas, o kartu gaunami naudingi taškai sudaro iki 70 % visų galimų rasti būdingųjų taškų.

Literatūra

1. Stanikūnas R., Bliznikas Z., Vaitkevičius H., Švegžda A. Objekto trimačio vaizdo atkūrimas iš jo dviejų kontūrų neturinčių dvimačių atvaizdų // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2002. – Nr. 1(36). – P. 43–47.
2. Schalkoff R. J. Digital image processing and computer vision // New York: Wiley, 1989. – P. 30–39.
3. Serackis A., Navakauskas D. Investigation of uncertainties in 3D reconstruction // Известия Белорусской инженерной академии. – Минск, 2005 (in press).
4. Roberts D. R., Marshall A. D. Viewpoint Selection for Complete Surface Coverage of Three Dimensional Objects // Proceedings of the British Machine Vision Conference. – Southampton, 1998. – Vol. 2. – P. 740–750.
5. Шмаков П. В., Колинб К. Т., Джакония В. Е. Стереотелевидение // Связь, 1968. – P. 22–27.
6. Dervinis D. Būdingų veido taškų išskyrimas dvimačiame vaizde // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2004. – Nr.5(54). – P. 18–22.
7. Harris C., Stephens M. A combined corner and edge detector // In Proceedings Alvey Conference, 1987. – P. 189–192.
8. Valantinas J., Morkevičius N. Smoothness Analysis of Two-dimensional Gray-level Images // Information technology and control – Kaunas: Technologija, 2000. – No.1(14). – P. 15–24.
9. Morkevičius N., Valantinas J. On the Application of Image Smoothness Estimates to Adaptive Coding of Gray-Scale Images // Information Technology and Control – Kaunas: Technologija, 2002. – No. 1(22). – P. 13–21.
10. Torr P. H. S. A structure and motion toolkit in Matlab // Microsoft Research, 2002. – P. 7–13.
11. Serackis A., Navakauskas D. Influence of object view angle to 3D stereo reconstruction // Scientific announcements of the Scientific-Technical Union of Mechanical Engineering. – Bulgaria, 2005 (in press).

A. Serackis, D. Navakauskas. Dviejų kamerų tarpusavio padėties įtaka trimačių vaizdų rekonstrukcijai // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2006. – Nr. 1(65). – P. 77–80.