Svarbus kriptografinių sistemų analizės etapas – matematinio modelio sudarymas ir šifro mazgų aprašymas diskretinėmis funkcijomis. Atliekant kriptoanalizę, diskretinė funkcija yra naudingas matematinis modelis, kuriuo galima pavaizduoti informacijos keitimą srautiniuose šifruose. Šis modelis patogus tuo, kad srautinius šifrus galima analizuoti diskretinės matematikos pagrindu. 
Įvadas
Svarbus kriptografinių sistemų analizės etapas – matematinio modelio sudarymas ir šifro mazgų aprašymas diskretinėmis, dažniausiai Bulio, funkcijomis. Atliekant kriptoanalizę, diskretinė funkcija yra naudingas matematinis modelis, kuriuo galima pavaizduoti informacijos keitimą srautiniuose šifruose. Šis modelis patogus tuo, kad srautinius šifrus galima analizuoti diskretinės matematikos pagrindu, prieš tai tinkamai įvertinus kriptografines Bulio funkcijos savybes. Bulio funkcija, susidedanti iš n kintamųjų, – tai n-matės vektorinės erdvės F2n atvaizdavimas vienmatėje erdvėje F2 = {0,1} [2]:
Svarbus Bulio funkcijų analizės metodas – Walsho transformacija Wf(u). Funkcijos f Walsho transformacija, esant vektoriui uЄF2n vadinama skaitinė vertė [2]:
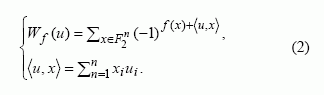
Viena iš esminių kriptografinių savybių yra subalansavimas. Reikalavimai subalansavimui remiasi Golombo postulatais. Funkcija f (x) vadinama subalansuota, jei
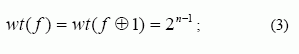
čia wt( f ) yra funkcijos f (x) Є F2n Hemingo svoris, t.y. skaičius x rinkmenų, tenkinančių lygybę f (x) = 1. Subalansuotos funkcijos Walsho transformacijos vertė, esant nuliniam vektoriui:
Kita kriptografinė Bulio funkcijos savybė yra netiesiškumas. Funkcijos tiesiškumas suprantamas kaip matematinio uždavinio efektyvaus sprendinio buvimas. Todėl kriptografinių sistemų netiesiškumas yra fundamentali ir neatskiriama savybė. Konkretus netiesiškumo traktavimas ir jį aprašantys parametrai gali būti įvairūs.
Dažniausiai netiesiškumas apibrėžiamas funkcijos Hemingo atstumu iki afiniųjų funkcijų visumos. Pagal Mebuso transformacijos teorema kiekvieną Bulio funkciją galima vienareikšmiškai išreikšti ANF (algebrinės normalinės formos) polinomu [4]:
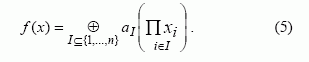
Polinomo laipsnis deg f – tai netiesiškumo laipsnis. Jei polinomo laipsnis deg f = 1, tai tokia funkcija vadinama afiniąja funkcija[4]:
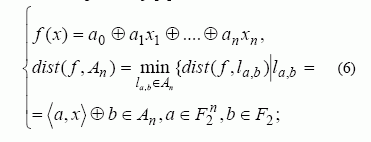
čia 
– skaliarinė sandauga.
Netiesiškumo parametras nusako galimybę
analizuojamąją funkciją pakeisti afiniuoju analogu. Šis
atstumas vadinamas funkcijos netiesiškumu ir žymimas
taip:
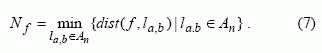
Funkcijos f Hemingo atstumas iki afiniųjų funkcijų dist( f , An ) [2] susijęs su Walsho transformacijos koeficientais tokia išraiška:
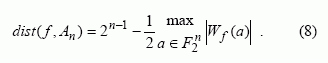
Remiantis tiesinės sandoros funkcijos apibrėžimu
įvesta absoliučiai netiesinių funkcijų sąvoka. Absoliučiai
netiesinė funkcija yra tada, kai 
. Ši savybė
absoliučiai netiesines funkcijas sutapatina su
kombinatorinėmis bent funkcijomis, todėl šios funkcijos
kriptografijoje vadinamos bent funkcijomis.
Bent funkcijos yra labai naudingos kriptografinės
funkcijos, kadangi jos tuo pat metu turi maksimalų
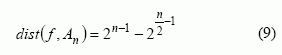
atstumą iki visų tiesinių funkcijų ir maksimalų 2n−2 atstumą iki visų funkcijų, turinčių tiesinę sandarą. Generatoriai, sukurti bent funkcijų pagrindu, yra atsparūs tiesinei sintezei. Kadangi Walsho transformacijos koeficientai yra sveikieji skaičiai, todėl maksimaliai netiesinės funkcijos egzistuoja tik esant lyginiam kintamųjų skaičiui.
Srautinio šifro modelio tyrimas
Dideliam kriptografiniam atsparumui pasiekti srautinių šifrų konstruktoriai naudoja mazgus postūmio registro judesio netolydumui didinti. Vienas tokių sprendimų yra R. Rueppelio pasiūlyta mažoritarinė LFSR pakopų sinchronizacija (1 pav.).
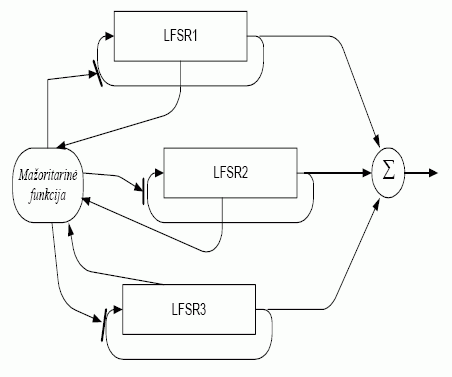
1 pav. LFSR pakopų sinchronizacija
Šis būdas įgyvendintas A5/1 šifre. A5/1 šifras yra išnagrinėtas ir jo kriptoanalizė atlikta, tačiau ji remiasi bendraisiais šifrų analizės metodais: gimimo dienos paradoksu, laiko ir atminties pakeitimo ataka, ypatingų padėčių ataka ir t. t., tai yra buvo pasinaudota konstrukciniais šifro trūkumais, bet nebuvo sudarytas šios schemos matematinis modelis, nenustatyta šifravimo gamos generuojančioji funkcija ir neįvertintos jos kriptografinės charakteristikos ir kriterijai.
Sukurkime šifrą, kurio LFSR pakopos būtų sinchronizuojamos mažoritarine funkcija , o šifro raktų erdvė pakankamai nedidelė, kad galėtume atlikti išsamią statistinę šio šifro analizę. Galimas tokios konstrukcijos pavyzdys pateiktas 2 pav.
Ši srautinio šifro schema turi trijų, keturių ir penkių skilčių ilgio LFSR. Registrų ilgiai ir jų atvadai parinkti taip, kad išėjimo gama, nesant mažoritarinės sinchronizacijos, turėtų didžiausią periodą. Pirmasis registras generuoja maksimalią ilgio seką, kurios periodas 7, antrasis atitinkamai – 15, trečiasis – 31 periodo seką. Tokio generatoriaus raktų ilgis 12 bitų, o visa raktų erdvė– 212 , arba 4096, skirtingi raktų variantai.
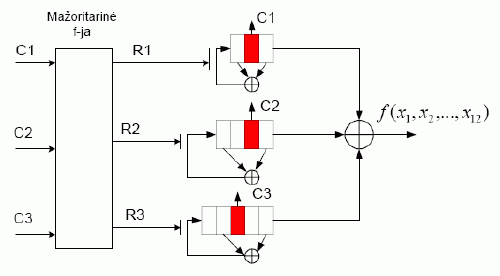
2 pav. Analizuojamoji srautinio šifro schema
Perrinkime visas galimas raktų kombinacijas ir atlikime generuojamos gamos statistinę analizę: apskaičiuokime generuojamos sekos periodą ir tiesinį kompleksiškumą Berlekamp ir Massey algoritmu. Rezultatus surašome į lentelę.
Sudarydami matematinį modelį, remsimės tik paskutinės skilties rezultatais, o kitus paneigsime dėl šių priežasčių:
1. 89 bitų ilgio sekos nagrinėjamoje grupėje yra kriptografiniu požiūriu stipriausios;
2. Likusios sekos – tai ypatingi atvejai: pirmojoje skiltyje yra tos raktų kombinacijos, kurių bent du registrai užpildyti nuliais, antrojoje skiltyje – kai trečiojo registro visos skiltys užpildytos nuliais , trečiojoje – kai antrojo, ir ketvirtojoje – kai trečiojo. Ypatingų atvejų susidarymo dažnis priklauso nuo registrų ilgių. Tikimybė, kad trumpiausio registro visos skiltys yra nuliai, lygi 1/2n, tad realiomis sąlygomis, kai registro ilgis viršija 20, ypatingų atvejų skaičius bus palyginti nereikšmingas.
Šis generatorius 3149 atvejais generuoja periodinę 89 bitų ilgio seką, kuri konkrečiam raktui skiriasi faze:
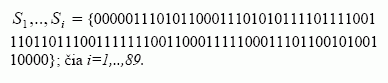
Norėdami rasti generuojančiąją sekos funkciją, tam tikslui analizuojamą schemą pakeiskime rekurentiniu generatoriumi, kuris generuotų tokią seką (3 pav.).
3 pav. Hipotetinis generatorius
Rekurentinės sekos, generuojančios funkcijos kintamųjų skaičių, apibrėžia ilgiausio pasikartojančio segmento ilgis generuojamoje sekoje. Randame ilgiausią pasikartojantį segmentą:{0001110101}. Jo ilgis yra 10 bitų, vadinasi, turi būti 11 inicialinių generuojančiosios sekos bitų.
Tokios sekos generuojančiosios funkcijos f (x1,...x11) didžiausias polinomo laipsnis būtų 11, o teisingumo lentelės verčių matrica turėtų 211 elementų, iš jų: nulių matrica [F0 ] – 38 elementus , vienetų matrica [F1] – 51 elementą, neapibrėžtų reikšmių matrica [Fd ] turėtų likusius 1959 elementus. Tokios funkcijos analizė yra ypač sudėtinga ir pareikalautų labai didelių skaičiavimo ir laiko išteklių.
Kriptografiniu požiūriu prasminga rasti tokią generuojančiąją funkciją, kuri generuotų seką, artimą nagrinėjamai (santykinis Hemingo atstumas < 0,5), o polinomo laipsnis būtų kiek galima mažesnis. Akivaizdu, kad 89 bitų periodinę seką generuotų funkcija, kurios kintamųjų skaičius būtų bent 7 ( 27 −1 > 89).
Transformuokime analizuojamąją seką, pakeisdami kai kuriuos sekos elementus taip, kad ilgiausias pasikartojantis fragmento ilgis neviršytų 7 bitų, o Hemingo atstumas tarp sekų būtų ne didesnis kaip 44. Galimas tokios sekos variantas:
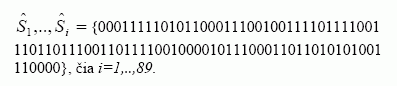
Šios sekos ilgiausio pasikartojančio fragmento ilgis
yra septyni bitai, o Hemingo atstumas nuo pradinės sekos
– 12 bitų. Tokią seką generuotų septynių kintamųjų Bulio
funkcija f (x1,..x7 ) , maksimalus polinomo laipsnis yra 7.
Šios funkcijos teisingumo lentelė yra 8× 27
matmenų. Bet kuri 8 bitų sekos 
atkarpa yra
funkcijos teisingumo lentelės viena eilutė , kurios pirmieji
septyni bitai – tai funkcijos argumentų vertės, o aštuntas
bitas – funkcijos vertė.
Tokių atkarpų kartu su cikliniu postūmiu yra 89, o neapibrėžtų verčių matrica turi 39 elementus, vadinasi, yra 239 skirtingų funkcijų, kurios generuoja tokią seką. Priskirkime visus neapibrėžtų verčių matricos elementus nulių matricai. Kaip žinome, kiekvieną visiškai apibrėžtą funkciją galime išreikšti unikaliu ANF polinomu:
čia xI – vienanaris, lygus
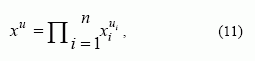
o au Є F2 – tai teisingumo lentelės elementas. Sudarę rekurentinės sekos teisingumo lentelę, išvedame sekos ANF:
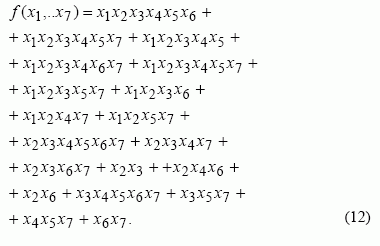
Įvertinkime funkcijos netiesiškumą Hemingo atstumu iki afiniųjų funkcijų. Išreikškime atstumą šios funkcijos Walsh ir Hadamard transformacijos koeficientais:
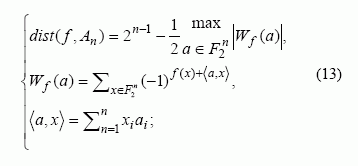
čia ai ir f (x) – tai funkcijos teisingumo lentelės atitinkami elementai. 4 pav. pateikti funkcijos f (x1,..x7 ) Walsh ir Hadamardo transformacijos rezultatai – funkcijos energinis spektras. Abscisių ašyje leksikografine tvarka atidėtos funkcijos argumentų vertės, ordinatėje – atitinkamas Walsho ir Hadamardo transformacijos koeficientas Wf (a) .
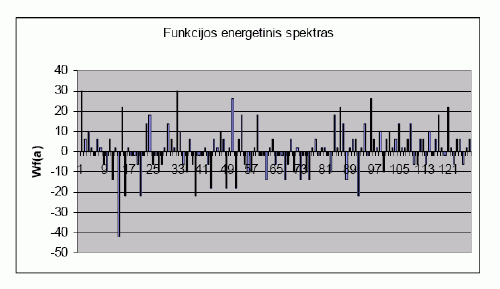
4 pav. Funkcijos energinis spektras
Matome, kad maksimali transformacijos |Wf (a) | vertė lygi 42, kai x1,..., x7 = {0,0,0,1,1,0,1}.
Apskaičiuojame netiesiškumą:
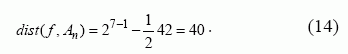
Dabar, žinodami funkcijos f (x1,..x7 ) netiesiškumą,
įvertinkime seką S1,.., Si generuojančios funkcijos
f (x1,...x11) netiesiškumą. Kadangi Hemingo atstumas
tarp dviejų sekų S1,.., Si ir 
yra 12 bitų, tai
akivaizdu, kad f (x1,...x11) atstumas iki afiniųjų funkcijų
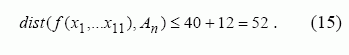
Matome, kad f (x1,...x11) nėra bent funkcija, kadangi maksimalus netiesiškumas
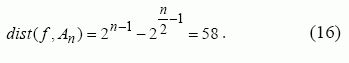
Išvados
Mažoritarinės funkcijos yra paprasto dizaino ir labai netiesiškos, todėl plačiai naudojamos srautiniams šiframs konstruoti. Atliktas tyrimas parodė kelis esminius tokių šifrų trūkumus. Generuojančioji funkcija yra nesubalansuota, t. y. gamoje yra „nuliukų“ ir „vienetukų“ disbalansas, todėl tokia seka yra jautri testinei analizei. Šifravimo gama yra ne maksimalaus 2N-1, o tik ~2(2/3)N bitų periodo, kur N – rakto ilgis, todėl ją keblu taikyti didesniems failams šifruoti. Tokio šifro generuojančioji funkcija nepriklauso bent funkcijų klasei, jos taikymas srautinių šifrų registrams valdyti neužtikrina maksimalaus netiesiškumo, todėl galima tokio šifro šifravimo gamos tiesinė sintezė. Mažoritarinės funkcijos neapibrėžtumų matrica turi 1959 elementus, vadinasi, egzistuoja 21959 funkcijų, kurios generuoja tokią seką, todėl tolesniam tyrimui svarbu turėti algoritmą mažiausio laipsnio funkcijos paieškai.
Literatūra
- Rueppel R.A. Security Models and Notions for Stream Ciphers // Cryptography and Coding 11, C. Mitchell, ed.- Oxford: Clarendon Press, 1992. – P. 213–230.
- Zhang X.M, Zheng Y. Normalized Measures for Cryptographic security // Journal of Universal Computer science. – 2002. – No. 1(5). – P. 316–333.
- Menezes, P. van Oorschot and S.Vanstone. Handbook of Applied Cryptography // by A., CRC Press, 1996. – P. 169–190.
- Pommerening K. Fourier Analysis of Boolean Maps. A Tutorial–Fachbereich Mathematik der Johannes-Gutenberg- Universitaet Saarstrasse 21 D-55099 Mainz.– 2003.– P. 3–41.
- Wegener, John The Complexity of Boolean Functions // Wiley & Sons Ltd., and B.G. Teubner, Stuttgart July 1987. ISBN: 0471 -91555-6. –P. 243–249.
P. Nefas, A.Vobolis. Mažoritarinės funkcijos kriptografinių savybių tyrimas // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2005. – Nr. 1(65). – P. 73–76.
