Kompiuterių sistemos išliekamumo modeliavimas

Įvadas

Šių dienų kompiuterinės sistemos yra sujungtos tarpusavyje ir nutolusios viena kitos atžvilgiu. Didėja saugumo reikalavimai, nes organizacijos yra labai priklausomos nuo savo kompiuterių tinklo. Kompiuterių sistemų pažeidžiamumas savo ruožtu taip pat neišvengiamai didėja, nes dėl sistemų sujungimo daugiau potencialių įsibrovėlių gali pasiekti kitas sistemas. Patirtis rodo, kad didinant kompiuterių sistemos saugumą negalima visiškai užtikrinti nepažeidžiamumo, todėl būtina praplėsti požiūrį į kompiuterių sistemos saugumą ir siekti, kad sistema išliktų darbinga nepaisant galimų atakų. Tinkama paslauga teikiama tada, kai ji visiškai atitinka sistemos funkciją [1, 2].

Sistemos saugumui, kuris tiesiogiai priklauso nuo saugumo mechanizmų, įvertinti patogu naudoti išliekamumo charakteristiką ir pagal ją nustatyti sistemos saugumo pokytį kintant ją veikiantiems veiksniams ir jos parametrams.

Išliekamumas – tai sistemos gebėjimas atlikti savo misiją, net jei ji yra puolama ar dalis jos nereikšmingų paslaugų yra sukompromituota [3]. Taigi išliekamumas – tai sistemos gebėjimas teikti kritines paslaugas net sėkmingo įsibrovimo atveju ir sugebėti atsikurti iki normalios būsenos atakai pasibaigus. Todėl reikia, kad sistema sugebėtų reaguoti į įvykius ir vertinti juos: atpažintų atakas, būtų atspari vienoms ir sugebėtų atsikurti po kitų poveikio. Sistemos išliekamumas apima tokias sritis kaip patikimumas, saugumas ir atsparumas trikdžiams.

Sistemos išliekamumui įvertinti tikslinga modeliuoti sistemą ir ją veikiančius incidentus ieškant santykio tarp išliekamumo ir apsaugos mechanizmų stiprumo (kuris tiesiogiai priklauso nuo jų kainos).

Incidentų atsiradimo aprašymas

Incidentams prognozuoti modeliuojame tikimybinį taškinį procesą, kur incidentai yra įvykiai, vykstantys atsitiktiniais laiko momentais. Incidentą sukelia viena ar kelios tuo pat metu vykstančios atakos. Incidento tipą pažymėkime jЄ{J}, incidento tikimybę – P(j). Tariame, kad incidentai pagal sunkumą gali būti 5 tipų: nuo labai sunkaus j=1 iki lengvo j=5. Incidento pasirodymo laikas yra t_k. Laiko tarpas tarp incidentų yra lygus τ_k. Įvykio tipas yra incidento parametras ir nusako incidento sunkumą ir tikimybę, kad tuo pačiu metu vyksta ne viena ataka. Incidentų tipų aibė yra dvimatė, nusakoma sunkumu j ir atakų skaičiumi n {J×N}.

Stochastinį taškinį sistemos funkcionavimo procesą [4] apibūdina pasiskirstymo funkcija:

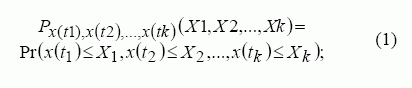
čia x(t₁), …, x(t_k) – atsitiktiniai (1, 2, ..., k) paslaugų funkcionavimo lygiai laiko momentais {t₁, t₂, …, t_k}, o {X₁, X₂, ..., X_k} – maksimalūs paslaugų funkcionavimo lygiai atitinkamai; t_iЄT, X_iЄR, i=1, 2, …, k. Su kiekvienu taškiniu procesu yra susietas skaičiavimo procesas N(t), t≥t0, rodantis bendrą taškų intervale [t₀, t) skaičių. Patogu tarti, kad procesas yra Puasono, tada tikimybių tankio funkcija

o pasiskirstymo funkcija

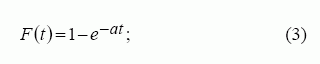
čia a – incidentų dažnis.

Kai naudojami hipotetiniai duomenys, reikia daryti keletą supaprastinimų. Dažnai pasirodo, kad incidentų atsiradimo procesas paklūsta Puasono skirstiniui. Kitais atvejais gali būti tikslinga naudoti Veibulio arba mišrių eksponenčių pasiskirstymus. Mišrių eksponenčių pasiskirstymas tinka, jei tuo pačiu metu sistemą atakuoja daugiau ir mažiau patyrę piktavaliai.

Sistemos išliekamumo vertinimo modelis pavaizduotas 1 paveiksle. Realius incidentus tenka porą kartų filtruoti ir apriboti iš abiejų pusių, kadangi yra laikoma, kad procesas prasidėjo prieš duomenų surinkimą ir nesibaigė tol, kol nebuvo baigti rinkti duomenys. Dėl to atsiranda papildomų paklaidų.

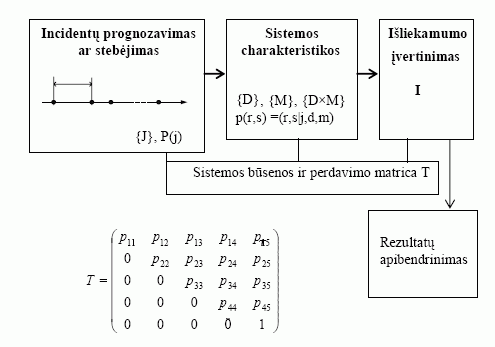
1 pav. Sistemos išliekamumo vertinimo modelis

Sistemos aprašymas

Sistema šiuo atveju nusakoma kaip jos įvairių parametrų visuma. Aprašoma architektūros erdvė {D} ir apsaugos mechanizmų erdvė {M}. Šių erdvių sandauga {D×M} yra vadinama konfigūracijos erdve. Kadangi sistema gali būti sudaryta iš daugelio skirtingos architektūros posistemių, tai turėtų būti nagrinėjami visi architektūrų variantai ir galimos konfigūracijos erdvės. Tarkime, kad yra dešimt apsaugos mechanizmų lygių m ir jų kaina C(m) didėja didėjant jų efektyvumui. Sistemos atsakas į incidentą yra incidento tipo ir konfigūracijos funkcija, išreikšta tikimybe, kad sistema iš pradinio būvio r pereis į kitą būvį s:

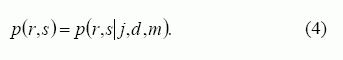
Taigi esant j tipo incidentui ir pradiniam sistemos būviui r, vėlesnė sistemos būsena s gali būti viena iš sistemos būvių aibės {S}: normali, puolama, sukompromituota, atkuriama ir nefunkcionuojanti. Realios būsenos bus skirtingos priklausomai nuo sistemos konfigūracijos ir reikalavimų jai.

Perėjimo matrica T per tikimybes susieja būvius r su s, esant duotiems j, d, m. Kiekvienas matricos T elementas yra sistemos, kurios architektūra d ir apsaugos mechanizmas m, perėjimo tikimybė į kitą (tikėtina sukompromituotą) būvį, kai vertinamas incidento tipas j.

Matricos struktūra tokia, kad būsenos yra išsidėsčiusios pagal sukompromitavimo lygį, t. y. nuo s=1 (normali) iki s=5 (nefunkcionuojanti). Įvykus incidentui, sistemos būvis pagerėti negali, todėl apatinis trikampis po įstrižaine lygus nuliui.

Matricos T elementams p(r, s), priklausantiems nuo j, d ir m galioja tokie teiginiai:

• p(r, s), kai s↓, kiekvienam s>r, j, m=const., t. y. to paties sunkumo incidentas ir ta pati apsauga, tolygi degradacija ir tikimybė, kad sistema pateks į gerokai blogesnę būseną, yra mažesnė už tikimybę patekti į šiek tiek blogesnę būseną;
• p(r, s), kai r↑, m=const., – tikimybė išlaikyti pradinę būseną r yra didesnė, jei ta būsena geresnė;
• p(1, s), kai j↓, kiekvienam s>1, m=const., – tikimybė likti normalios būsenos yra didesnė, jei incidentas lengvesnis;
• p(r, r), kai m↑, kiekvienam r, j=const., – degradacijos tikimybė mažesnė, jei apsauga stipresnė;
• p(r, s), kai n↑, kiekvienam s>r, kitkas=const., – degradacijos tikimybė didėja didėjant atakų skaičiui;
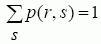• kiekvienam r – sistema turi būti kokio nors būvio.

Jei perėjimo tikimybės žinomos kiekvienu atveju, duomenis galima įvesti tiesiai į matricą, jei ne – galima generuoti perėjimo tikimybių matricos elementus p(r, s) arba juos apskaičiuoti įvertinant tarpines sistemos būsenas (reakciją į atakos epizodus). Perėjimo matrica yra sudėtinga, nes tikimybių erdvė: S²×J×D×M yra gana didelė. Todėl sistemą būtina apriboti.

Pradžioje galima nagrinėti vienos architektūros (D) sistemą. CERT teigia, kad laikas tarp incidentų bendruoju atveju yra maždaug mėnuo, o atkūrimo laikas daug trumpesnis. Todėl galima tarti, kad sistema, prieš įvykstant naujam incidentui, yra visiškai atkurta, o jos pradinis būvis nepažeistas r=1. Kai sistema yra sukompromituota, modelis leidžia įvertinti naują incidentą. Modeliuojant tokią sistemą reikia atsižvelgti į sistemos būsenų perėjimo laikus.

Nesant pradinių duomenų, galima sukurti tokį incidentų generavimo modelį p(1, s) [3]:

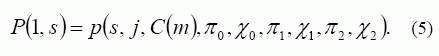
o kai s>1,

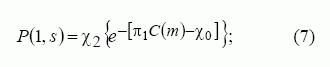
čia π₁ ir χ₁ yra formos koeficientai, nusakantys ryšį tarp perėjimo tikimybių ir apsaugos mechanizmų kainos, π₂ = π₂ ( j) = π₃ j – tiesinė j funkcija, χ₂ = χ₂ ( j, s) = = χ₃((7 − s)−0,35 j) – tiesinė s ir j funkcija.

Koeficientas χ₂ aprašytas taip, kad labiau priklausytų nuo kito sistemos būvio s, o ne nuo incidento parametro (j). Skalės koeficientai π₃ ir χ₃ parenkami taip, kad atspindėtų pagrįstas perdavimo funkcijų vertes, atsižvelgiant į esamus apribojimus. Padėties koeficientai π₀ ir χ₀ lygūs nuliui, o kitus koeficientus modeliavimo metu reikėtų keisti tiriant jų įtaką.

Tai yra paprastos, bet plačiai naudojamos funkcijų formos su įgaubiančiosiomis ir išgaubiančiosiomis dedamosiomis, atspindinčios mažėjančią atakų įtaką stiprėjant apsaugai, t. y. didėjant kainai.

Išliekamumo įvertinimas

Išliekamumas – tai sistemos gebėjimas priešintis atakoms ir funkcionuoti tam tikru lygiu po įvykusio incidento. Naujas būvis s bendruoju atveju yra sukompromituotas ir jame sistema laukia, kada bus atkurtas normalus darbas. Taigi sistemos išliekamumas yra naujo būvio darbingumo laipsnio ir visiško darbingumo santykis. Išliekamumas gali būti skaičiuojamas kiekvienai sistemos teikiamai paslaugai. Jei ta paslauga nepakito, tai išliekamumo I vertė bus lygi 1, jei paslauga nutraukta, jo vertė lygi 0, kitos vertės išsidėsčiusios tarp jų.

Tarkim φ(s, k) bus laipsnis, iki kurio paslauga k išliko s būvio, o w(k) – paslaugos svorio koeficientas. Tada išliekamumas gali būti išreikštas:

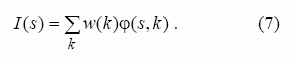
Būvių aibė {S} žinoma, o nustačius φ(s, k) kiekvienam s ir k, galima surasti vidutinį lygį, iki kurio paslauga k išlieka s būvio.

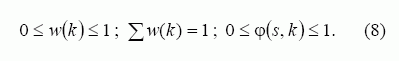
Galima vertinti santykinį, minimalų ar kitokį sistemos išliekamumą.

Geriausia įvesti svorio koeficientus w(k), kurie parodytų, kaip naudojamasi paslauga. Gali būti mažai naudojamos, bet svarbios paslaugos, todėl {K} verta skirstyti į du poaibius: vieną kritinių paslaugų {K1}, kitą nekritinių {K2}. Nekritinių ir retai naudojamų paslaugų atmesti neverta, nes jų pažeidžiamumas gali kelti gana didelę grėsmę sistemos išliekamumui. Remiantis išsakytomis prielaidomis galima užrašyti tokią išliekamumo išraišką, kurioje daugyba užtikrina, kad jei kritinė paslauga bus nutraukta ir φ`(s, k) bus lygi nuliui esant bet kuriam k, tai išliekamumas irgi bus lygus nuliui, o nekritinės paslaugos gali būti nutrauktos:

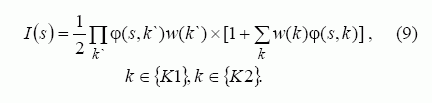
Realiose situacijose reikia surūšiuoti visus galimus sukompromitavimo variantus, kurie gali atsirasti sistemoje dėl žinomų ir nežinomų pažeidžiamumų. Tarkim, tikimybė, kad paslauga k bus sukompromituota iki lygio x, dėl j tipo incidento bus p_k,j(x). Tada galima skaičiuoti visų paslaugų bendrą susikompromitavimą po kiekvieno incidento, arba supaprastinti analizę ir tarti, kad nustatomas susikompromitavimas E[x(k,j)] esant duotiems j,

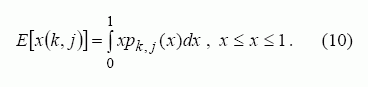
Tada numatomas išliekamumas, kuris patogiausias modeliuojant, bus:

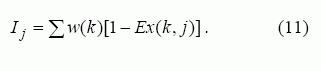
Išliekamumo modeliavimo procesas

Pagal aprašytą išliekamumo vertinimo modelį galima tirti sistemos elgseną viso atakos epizodo metu [5], t. y. sugeneravus incidentą, laukiama puolamos sistemos reakcijos, (įvertinant jos išliekamumą, priklausantį nuo apsaugos mechanizmų).

Modeliuojant parenkamos pradinės vertės: a – incidentų dažnis, υ – atakų n pasiskirstymo parametras, J – bendras incidentų tipų skaičius, P(j) kiekvieno incidentų tipo atsiradimo tikimybė, M – bendras apsaugos mechanizmų skaičius, C(m) – kiekvieno apsaugos mechanizmo kaina, S – bendras sistemos būsenų skaičius.

Modeliuojama taip: nustatoma incidentų tikimybių tankio funkcija f(t), generuojamas incidentas, t. y. atsitiktinai generuojama (t,j,n)|f(t),P(j),g(n). Generuojamas naujas sistemos būvis, remiantis matrica T(j,d,m). Skaičiuojamas išliekamumas. Kartojama, kol bus pasiektos baigimo sąlygos. Tai gali būti nustatytas laiko tarpas arba incidentų skaičius. Fiksuojamos gautos vertės: p(j), C(m), I_laukiamas|a,π₁,χ₁,π₃,χ₃. Verta keisti apsaugos mechanizmų skaičių ir įtaką. Tikslinga braižyti išliekamumo priklausomybės nuo kainos kreivę. Būtina įvertinti galimas paklaidas.

Modeliavimo algoritmas pateiktas 2 paveiksle. Modeliuojant buvo remiamasi tokiomis prielaidomis: saugumo mechanizmų kaina tiesiai proporcinga jų stiprumui: C(m)=10m. Tyrimo pradžioje sistema yra parengta darbui ir be klaidų sukonfigūruota, todėl tikimybė, kad atakos metu ji liks pradinio būvio p(1,1), yra didelė ir labai priklauso nuo incidento sunkumo j. Tikėtina, kad teisingą pradinę konfigūraciją ir atsparią architektūrą turinčios sistemos lengvi incidentai nepaveiks net jei ji neturės apsaugos mechanizmų.

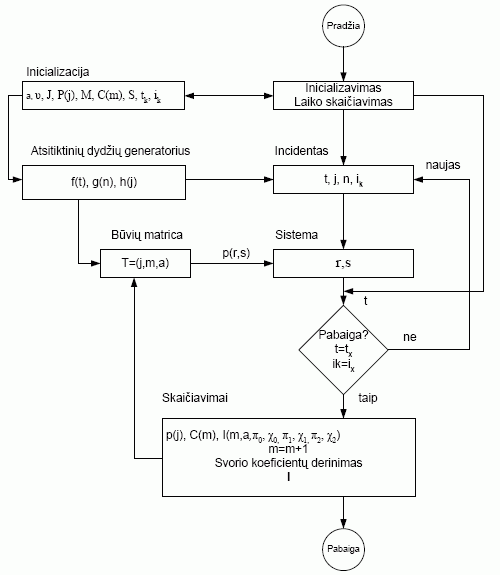
2 pav. Išliekamumo modeliavimo algoritmas

Tarkime, kad sistemą veikia Puasono skirstiniui paklūstančios dviejų tipų atakos: labai sunkios ir sunkios. Tuo pat metu vyksta tik viena ataka, tikimybė, kad bus tam tikro sunkumo ataka, yra lygi P(1)=P(2)=0,5, incidentų dažnis a=1,5. Tiriama sistema yra normalaus būvio (s=1) ir po kiekvieno incidento iki kito sistema suspėja sugrįžti į pradinę būseną. Tiriame sistemos perėjimą iš normalios būsenos (s=1) į sukompromituotą (s=3). Tikimybė p_{1, 3}(m, s, j) priklauso nuo apsaugos mechanizmo m, būsenos s, į kurią sistema pereina, ir incidento sunkumo j.

Įtakos turi ir kalibravimo koeficientai. Jie parinkti tokie, kad gaunami rezultatai turėtų prasmę. Apskaičiavus sistemos būsenos kitimo tikimybę p_{1, 3}(m, s, j) randamas numatomas išliekamumas (3 pav.).

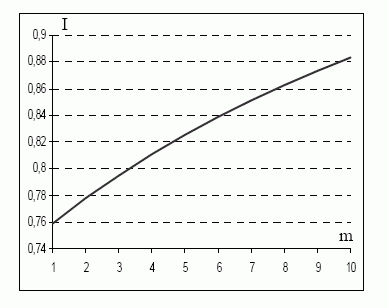
3 pav. Numatomo išliekamumo priklausomybė nuo apsaugos mechanizmų stiprumo

Iš išliekamumo priklausomybės nuo apsaugos mechanizmo stiprumo I(m) matyti, kad, kaip ir buvo tikėtasi, stiprėjant apsaugos mechanizmams, išliekamumas didėja, pastebima, kad išliekamumas net esant silpnesniems apsaugos mechanizmams yra didelis ir jiems stiprėjant pradžioje didėja sparčiau.

Išvados

1. Išliekamumas yra bendra skaitinė sistemos sugebėjimo išlikti po atakų charakteristika, vertinga lyginant sistemas ir apsaugos mechanizmus. Siekiant apsaugoti sistemą reikia naudoti platų apsaugos mechanizmų spektrą, juos tikslinga išdėstyti saugumo perimetre.
2. Gauti rezultatai rodo, kad teisingos pradinės konfigūracijos ir atsparios architektūros sistemos lengvi incidentai nepaveiks net jei ji neturės apsaugos mechanizmų.
3. Naudojantis modeliu galima gauti išliekamumo priklausomybę nuo apsaugos mechanizmų stiprumo ar jų kainos. Iš išliekamumo priklausomybės matyti, kad išliekamumas tuo geresnis, kuo lengvesnės atakos ir kainai didėjant pradžioje jis auga sparčiau.

Literatūra

1. Garšva E., Skudutis J. Saugių sistemų kūrimo tendencijos // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2004. – Nr. 6(55). – P. 43–48.
2. Avižienis A., Laprie J. C., Randell B. Basic concepts and taxonomy of dependable and secure computing // Dependable and Secure Computing. – 2004. – Vol. 1. – P. 11–33.
3. Moitra S. D., Konda S. L. A Simulation Model for Managing Survivability of Networked Information Systems. 2000. www.cert.org/research/00tr020.pdf
4. Banks J., Carson J. S., Nelson B. L., Nicol D. M. Discrete- Event System Simulation. – Prentice Hall, 2000. – 600 p. 5. Linger R. C., Lipson H. F., McHugh J., Mead N. R., Sledge C. A. Life-Cycle Models for Survivable Systems. 2002. www.cert.org/archive/pdf/02tr026.pdf
5. Moore A. P., Ellison R. J., Linger R. C. Attack Modeling for Information Security and Survivability. 2001. www.cert.org/archive/pdf/01tn001.pdf
6. Linger R. C., Mead N. R., and Lipson H. F.. Requirements Definition for Survivable Network Systems. www.cert.org/archive/pdf/icre.pdf

E. Garšva. Kompiuterių sistemų išliekamumo modeliavimas // Elektronika ir elektrotechnika. – Kaunas. Technologija, 2006. – Nr. 1 (65). – P. 56–59.