Šiais metais tik ir girdime apie per daug išpūstus „labai baisius“ pažeidžiamumus: pradžioje buvo Dan Kaminsky su DNS dizaino klaidomis, dabar internetą užlenkti žada keli TCP/IP steko tyrinėtojai. Tačiau DNS serverių eksploatacija bei priešiškai nusiteikusių serverių gesinimas vis tiek nedaro tavęs interneto valdovu, galbūt yra kitas būdas?
Šiais metais tik ir girdime apie per daug išpūstus „labai baisius“ pažeidžiamumus: pradžioje buvo Dan Kaminsky su DNS dizaino klaidomis, dabar internetą užlenkti žada keli TCP/IP steko tyrinėtojai. Tačiau DNS serverių eksploatacija bei priešiškai nusiteikusių serverių gesinimas vis tiek nedaro tavęs interneto valdovu, galbūt yra kitas būdas?
Iš tiesų parašyti šia tema mane paskatino ne tik perdėtas dėmesys ir panika dėl šiemet aptiktų pažeidžiamumų, kurių pradžioje nenorima atskleisti „nes ateis interneto galas“, o kai jie atskleidžiami, pasirodo, jog internetas dar kurį laiką pagyvens (o reklaminė kampanija pasisekė gerai). Užsiėmęs svetainės atnaujinimo darbais ir paskendęs praeities apmąstymuose prisiminiau dar Critical.lt ištakose užduotą klausimą kolegai: „Povilai, o kaip tu užvaldytum internetą?“ – paklausiau aš. Šis pamąstė, išpūtė cigaretės dūmą ir tuomet prasidėjo ilga diskusija, kurios esmę pamėginsiu ir išdėstyti savo tekste.
Pradžioje šiek tiek teorijos – apibrėžkime kas yra parazitiniai skaičiavimai. Peržiūrėję nedidelį straipsnį Wikipedijoje matome, kad parazitiniai skaičiavimai yra programavimo technika, sukonkretinant – saugumo pažeidžiamumas, leidžiantis vienam objektui (sistemai, programai t. t.) išnaudoti kito objekto resursus pernelyg sudėtingoms operacijoms atlikti jam to nežinant. Na mano suformuotas apibrėžimas matyt nepretenduoja būti labai tiksliu ir aiškiu, tačiau ir pati parazitinių skaičiavimų problema yra pakankamai delikati.
Sakykime, kad mums reikia atlikti kažkokį sudėtingą matematinį skaičiavimą, pavyzdžiui sveikųjų skaičių faktorizavimą – skaičių skaidymą į daliklius kuriuos sudauginus atgal gaunamas originalus skaičius. Šiuo metu nėra žinomas nei vienas efektyvus algoritmas šiai matematinei užduočiai, todėl ji yra naudojama viešojo rakto kriptografijoje, pseudo-atsitiktinių skaičių generatoriuose ir kituose algoritmuose kuriems reikia problemos kurios išsprendimui reiktų ypač daug skaičiavimo galios. Tačiau nesu matematiškai stiprus ir noriu kuo paprasčiau tai pavaizduoti tad tarkim, jog mums reikia sudėti keturis skaičius. Kadangi pavyzdys tik teorinis, įsivaizduokime, kad keturių skaičių sudėtis mums yra labai sudėtinga operacija, kuri užtrunka daug laiko. Dabar tarkime, kad egzistuoja kažkoks tai tinklo protokolas, kuris galėtų būti skirtas duomenų distribucijai vidiniame tinkle ar bet kokiam kitam mūsų sugalvotam tikslui, tačiau savo darbo eigoje sudeda du mūsų pateiktus skaičius ir vėliau grąžina rezultatą. T. y. protokolo paskirtis yra vienokia, tačiau to tikslo įgyvendinimo metu yra sudedami mūsų skaičiai.
Taigi mums reikia sudėti keturis skaičius ir tai mūsų įsivaizduojamame iškreiptame pasaulyje yra sudėtingiau nei nusiųsti keletą paketų tinkle. Todėl kadangi mes žinome, jog galime priversti kitus tinkle egzistuojančius kompiuterius apskaičiuoti dviejų skaičių sumą, mes išskaidome keturių skaičių sudėties problemą į tris mažesnes: (1+2)+(3+4). Sukuriame parazitą, kuris naudodamasis šiuo atveju išgalvotu protokolu paprašys atlikti mums per sudėtingas operacijas kitų kompiuterių:
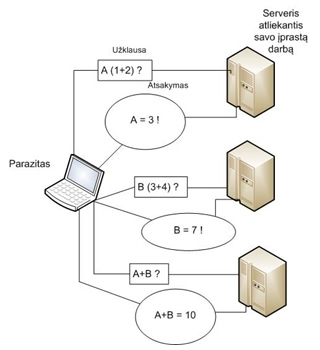
Šiame nerealistiškame pavyzdyje parazitinius skaičiavimus naudojantis kompiuteris išskaidė jam per sudėtingą užduotį į keletą mažesnių ir išsprendė jas kitų kompiuterių pagalba. Kadangi jam siųsti paketus yra lengviau nei sudėdinėti skaičius (na jie galėtų būti labai dideli ar pan.) jis imituodamas darbą jam prieinamu protokolu, kurį vykdant kažkuriuo metu yra sudedami du skaičiai ir siuntėjui grąžinamas sudėties rezultatas apskaičiavo jam reikiamą išraišką naudodamasis kitų sistemų resursais. Be to, tos sistemos nežinojo, jog vykdo skaičiavimus kitam kompiuteriui. Tai ir yra klasikinė parazitinių skaičiavimų teorijos idėja. Aišku moksliniuose darbuose ši idėja yra iliustruojama kitaip – TCP paketų dėka sprendžiant 3-SAT problemą. Savo pavyzdyje bandžiau tai supaprastinti, tam, kad nereiktų gilintis į tai, kas yra 3-SAT problema, bet jei man tai nepavyko – patarčiau susipažinti su kitais šaltiniais :)
Taigi nors ir yra moksliškai įrodyta, jog parazitinių skaičiavimų problema tikrai egzistuoja, tačiau tradicinėje aplinkoje nėra adekvataus būdo šiuo pažeidžiamumu pasinaudoti. Iš tiesų tai yra gerai, kadangi jei priverstume kitus kompiuterius jiems to nežinant vykdyti mums iš ties naudingus skaičiavimus – taptume didžiausios pasaulyje skaičiavimo mašinos, geriausiu atveju sudarytos iš visų interneto kompiuterių, tinklo įrenginių ir t. t. valdovais.
Grįžkime prie mūsų ramaus 2005-ų vasaros vakaro: juokais pradėtoje diskusijoje išsiaiškinome, kad šiuolaikiniame internete be tinklo protokolų išnaudojimo yra ir kitų būdų parazitiniams skaičiavimams atlikti ir vienas iš jų – interneto puslapiai.
Šiuolaikiniai WEB programuotojai turi daugybę įrankių savo idėjoms vartotojo pusėje išreikšti – tai „java appletai“, „javascript“, „flash“, „activex“, „silverlight“ ir kt. technologijos. Visos šios technologijos gali pasitarnauti parazitiniams skaičiavimams atlikti – jų pagalba galima kažką įdomaus apskaičiuoti, o taip pat ir kažkur perduoti rezultatą. Taigi imkime kaip pavyzdį paplitusią užduotį – MD5 „hashų“ parinkimą. Tai iš tiesų yra sudėtingas ir ilgai trunkantis procesas, reikalaujantis daug sistemos resursų. Turime sudėtingą skaičiavimą, kuris gali būti išskaidytas į smulkesnius etapus – jeigu procese dalyvautų ne vienas o keletas kompiuterių, mes galėtume duoti kiekvienam išspręsti dalį užduoties – vienam perrinkti vieną dalį visų galimų reikšmių, kitam – kitą ir t. t. Kuo daugiau kompiuterių spręstų šią problemą dalimis – tuo greičiau gautume rezultatą.
Bet mes po ranka neturime didelės masės kompiuterių – tai ištaisyti mums padės parazitiniai skaičiavimai. Šios užduoties sprendimo koncepcija atrodo taip: sukuriamas serveris, kuris bus skirtas užduočių padalinimui. Bendru atveju jis perduos klientui-parazitui ieškomą „hashą“ ir dalį jo reikšmių lauko, kurią reikia apskaičiuoti. Tuo tarpu klientas yra aktyvuojamas, prisijungia prie mūsų serverio, pasiima ieškomą „hashą“ ir savo skaičiavimų dalį. Gavęs šiuos duomenis jis ima perrinkinėti jam patikėtus variantus ir lyginti juos su turimu „hashu“. Jei sutapimo nerandama – pranešama, jog baigtas paskirtos dalies perrinkimas, gaunama nauja porcija ir procesas tęsiasi. Radus reikiamą reikšmę – siunčiamas atitinkamas džiaugsmingas atsakymas serveriui ir procesas nutraukiamas.
Tai tėra „griaučiai“, kadangi atsiras joje nenumatytų situacijų, kuomet klientas nespės perrinkti savo dalies arba dėl blogo ryšio grąžins sugadintą paketą ar pan.
Turime šiokią tokią idėją – pereikime prie realizacijos. Iš principo, ši mintis techniškai galėtų veikti ten, kur išeina įterpti mūsų sukurtą kodą. Praktikoje, deja (o gal ir kaip tik gerai), situacija nėra rožinė: sakykime mes įterptume savo parazitinį kodą kažkokioje mažai lankomoje svetainėje – mažas lankomumas reiškia ir mažą kompiuterių-dalyvių skaičių, todėl mes turime jį įkišti kažkur, kur lankosi daug būsimų paskirstyto skaičiavimų tinklo dalyvių. Kitas aspektas yra tai, kad iš didelio dalyvių skaičiaus nebūtinai išeis galingas skaičiavimo tinklas, jei jie mūsų svetainėje užsibūna vos kelias ar keliolika sekundžių. Todėl mes suinteresuoti, kad lankytojai mūsų išnaudojamoje svetainėje užsibūtų kuo ilgiau.
Akivaizdu, kad jeigu turėtume labai lankomą svetainę, tokią kaip „YouTube“ ar kiti lankomi filmukų puslapiai, kuriuose yra daug lankytojų ir jie užsibūna ilgai, po kelias minutes ar net valandas (jei išeina kur nors, bet palieka atvirą naršyklės langą) tai visa ši koncepcija veiktų. N milijonų lankytojų per dieną x 5 minutės / iš kažkiek tai kombinacijų per minutę.
Tačiau mes nevaldome „YouTube“. Neturime mes ir kokio kiek mažesnio lankomo resurso. Tačiau galimybių vis dar yra – papildomai galime pasinaudoti įvairių reklamą talpinti siūlančių svetainių ar tarpininkų paslaugomis. Sukuriame niekam neįdomią, neviliojančią reklamą apie bebrų dirbtinį apsėklinimą, už kurią mokėsime tik jei kas nors ant jos nuspaus ir aišku, mes suinteresuoti, kad ji bus patalpinta visiškai dėmesio netraukiančioje, nepastebimoje svetainės išdėstymo vietoje, tačiau figūruos lankomuose puslapiuose. Dar galima bandyti nusipirkti vietą svetainėje, kurioje bus talpinamas mūsų kodas iš įvairių svetainių, talpinančių piratinius filmus peržiūrai „online“ režimu. Taip gausime gal ne tiek daug vartotojų, bet jie dirbs mūsų darbą ilgai ir dar grįš vėliau!
Dar vienas, net gi pragmatiškesnis, būdas – „flash“ ar „javascript“ paremtų žaidimų svetainės. Turbūt ne vienas skaitytojas norėdamas prastumti laiką žaidė kokį nors užkrečiantį, ypač paprastą „flash“ žaidimą. Tokio tipo svetainės pritraukia milijonus vartotojų ir suėda milijonus laisvalaikio bei darbo valandų. Didelę „flash“ žaidimų kolekciją, nors ir neautorizuotų, surinkti paprasta. Įterpti į kiekvieną žaidimą parazitinio kodo gabalą ne taip paprasta, bet tikrai įmanoma. Be abejo galima ir neįterpinėti kodo į kiekvieną žaidimą, o naudoti atskirą kenksmingo kodo aplikaciją, tačiau tokiu atveju parazitinis kodas išplistų ir už mūsų valdomo tinklalapio ribų, nes tarp tokio tipo svetainių populiarios žaidimų vagystės, kurių metu viena svetainė nukopijuoja žaidimus iš kitos. Taipogi, platinant kodą žaidimuose būtų sutaupoma labai daug interneto srauto palyginus su video svetainėmis.
Taip pat jei nebijome pažeisti įstatymų, galime prisiminti, jog lankomos svetainės (pačios lankomiausios gal ir neturi, tačiau kiek žemesnį reitingą turinčiose tikrai rasi) turi XSS pažeidžiamumų, leidžiančių įterpti mūsų piktą kodą ir taip gauti didelį dalyvių skaičių, galų gale galima nebrangiai įsigyti turkų hakerių paslaugų – jie įterps mūsų norimą kodą į šimtus svetainių. (aišku parazitiniai skaičiavimai įsilaužus turi mažiau prasmės, kadangi mes galėtume tiesiog platinti kenksmingą programinę įranga ir naudotis užvaldytais resursais kaip mes norim). Kalbant apie XSS dar vienas būdas platinti parazitinį kodą – XSS kirminai. Prieš kelis metus sukurtas, „MySpace“ tinklalapyje plitęs, kirminas „Sammy“ per 20 h „apkrėtė“ apytiksliai 1 milijoną vartotojų. 1 milijonas aukų kurie kiekvieną kart apsilankę „MySpace“ vykdytų parazitinį kodą turėtų tikrai daug skaičiavimo galios.
