Įvadas
Netiesinės automatinės sistemos elgseną, pereinant iš tam tikros pradinės būsenos į stabilios pusiausvyros būseną arba į stabilų priverstinį režimą, apibūdina jos pereinamoji reakcija. Šios reakcijos kokybei vertinti galima panaudoti sistemos santykinio stabilumo charakteristikas, kurios leidžia nustatyti pereinamosios reakcijos formą ir greitį, jos svyravimų dažnį, slopinimo laipsnį ir kt.
Tiesinėse sistemose šie įverčiai turi tikslią analitinę išraišką, nustatančią sistemos parametrų ir jos pereinamosios reakcijos kokybinių charakteristikų tarpusavio sąsajas. Netiesinėse sistemose tokios galimybės nėra, todėl valdymo praktikoje pasitenkinama tik srities, kurioje randasi šie įverčiai, ribų nustatymu.
Pagrindinis įrankis, sprendžiant tiesinių automatinių sistemų analizės ir sintezės uždavinius, šiuo metu yra šaknų hodografo metodas [1]. Šio efektyvaus metodo nauda visų pirma yra ta, kad jis labai paprastas, kai šaknų hodografui konstruoti panaudojami šiuolaikiniai sistemos lygčių sprendimo metodai ir jų modeliavimo priemonės. Be to, taikant šaknų hodografo metodą, gaunama tiriamos automatinės sistemos valdymo charakteristikų kokybinė išraiška ir efektyvi kiekybinė priemonė, teikianti apie sistemos valdymo procesą daugiau informacijos negu kiti metodai.
Todėl natūralu bandyti analogišką metodiką panaudoti ir sistemose su netiesiniais elementais. Sistemos sandaros požiūriu, toks bandymas gali būti atliekamas palyginti paprastai, nors netiesinis elementas šiek tiek apriboja automatinių sistemų struktūrinių schemų algebros taisyklių taikymą. Tačiau sistemos charakteristinių lygčių (ir jų sprendinių priklausomybės nuo netiesiškumo charakteristikų) požiūriu toks bandymas yra gerokai sudėtingesnis: charakteristinė lygtis ir jos šaknų hodografo kategorija reikalauja, kad sistemos netiesiškumas būtų aprašomas jo kauzalinės priklausomybės multiplikatyviąja išraiškos forma. Be to, šią priklausomybę būtina susieti su sistemos tiesinių elementų kompleksinės arba dažnių srities modeliais. Siekiant patenkinti šiuos reikalavimus valdymo praktikoje, netiesinį reiškinį (elementą), taikant harmoninio linearizavimo principą [2], galima aproksimuoti apytiksliu tiesiniu modeliu – ekvivalentiniu kompleksiniu stiprinimo koeficientu.
Harmoninis linearizavimas yra specialiai pritaikytas netiesinių automatinių sistemų periodiniams režimams tirti. Jo taikymo valdymo praktikoje pagrindinė sritis – ribinių ciklų prognozavimas, jų parametrų identifikavimas ir šių ciklų stabilumo analizė [3].
Šaknų hodografo konstravimas
Tipine struktūrine schema (1 pav.) atvaizduotos harmoniškai linearizuotos sistemos ekvivalentinė charakteristinė lygtis yra tokia [2]:
čia N(A) – netiesinio elemento ekvivalentinis kompleksinis stiprinimo koeficientas;
G(s) – sistemos tiesinės dalies perdavimo funkcija;
A – netiesinio elemento kvaziharmoninio įėjimo signalo e(t) amplitudė.
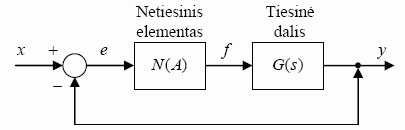
1 pav. Sistemos struktūrinė schema
Tiriant šios sistemos valdymo procesą, reikia visų pirma nustatyti šio proceso kokybinių charakteristikų ir netiesinio elemento įėjimo signalo amplitudės A sąsajas. Šį uždavinį galima išspręsti konstruojant (1) charakteristinės lygties šaknų hodografą, t. y. nustatyti šios lygties šaknų migravimo kompleksinėje s = σ + jω plokštumoje trajektorijas, kai varijuoja netiesinio elemento įėjimo signalo amplitudė A. Tuo tikslu (1) lygtis, tiesinės dalies perdavimo funkciją išreiškus dviejų kompleksinio kintamojo daugianarių santykiu, t. y. G(s) = N(s) / D(s) , pertvarkoma taip:
Akivaizdu, kad (2) charakteristinės lygties šaknų dislokacija kompleksinėje s plokštumoje priklausys nuo koeficiento N(A) , kuris bendruoju atveju yra kompleksinė ir įėjimo signalo e(t) dažniui ω invariantinė funkcija, apibrėžiama tokia išraiška [2]:
čia a(A) ir b(A) – netiesinio elemento išėjimo signalo f (t) Fourier transformantės;
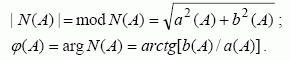
Taigi harmoniškai linearizuotos sistemos (1 pav.) šaknų hodografui konstruoti galima naudoti tokios formos charakteristinę lygtį:
Joje bendruoju atveju varijuoja du nelygūs nuliui netiesinio elemento ekvivalentinio kompleksinio stiprinimo koeficiento parametrai – modulis K1 = | N(A) | ir argumentas K2 = φ (A) . Šios sistemos charakteristinių šaknų padėtį (esant visoms varijuojamų parametrų K1 ir K2 reikšmėms) galima nustatyti ieškant kompleksinės s plokštumos taškų s = si (A) , tenkinančių (4) charakteristinę lygtį. Taigi taškai si turi būti šios charakteristinės lygties sprendiniai ir tuo pat metu tenkinti šias dvi sąlygas [1]:
− šaknų hodografo modulio sąlygą:
− šaknų hodografo kampų sąlygą:
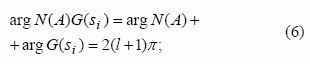
čia l = 0, ±1, ± 2,...
Atsižvelgiant į tai, kad netiesinio elemento ekvivalentinio kompleksinio stiprinimo koeficiento (3) išraiškoje esančios Fourier transformantės a(A) ir b(A) paprastai yra gana sudėtingos priklausomybės [2], linearizuotos sistemos šaknų hodografą, taikant charakteristinių šaknų kontūrų metodą [1], reikia konstruoti dviem etapais: sudaryti atskiras šaknų migravimo trajektorijas (nuo dviejų nepriklausomų varijuojamų parametrų K1 ir K2 ), o paskui ieškoti taškų si (A) . Taigi šį daugiaparametrį uždavinį galima spręsti tokia veiksmų seka:
1 žingsnis. Harmoniškai linearizuotos netiesinės sistemos ekvivalentinė charakteristinė lygtis 1+ N(A)G(s) = 0 išreiškiama tokia forma, kurioje varijuojamieji parametrai K1(A) ir K2 (A) yra nuo kompleksinio kintamojo s nepriklausantys multiplikatyvieji parametrai, t. y.
2 žingsnis. Vienas iš varijuojamų parametrų, pavyzdžiui, K2 , prilyginamas nuliui, o (7) charakteristinė lygtis perrašoma taip:
3 žingsnis. Konstruojamas (8) charakteristinės lygties šaknų hodografas. Akivaizdu, kad jo forma priklausys nuo funkcijos K1N1(s) / D(s) polių ir nulių dislokacijos s plokštumoje.
4 žingsnis. (7) charakteristinės lygties abi puses dalijant iš narių, nepriklausančių nuo K2 , sumos, suformuojama parametrizuotoji charakteristinė lygtis
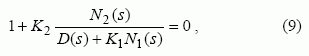
kurioje parametro K1 reikšmės yra fiksuotos ir nelygios nuliui.
5 žingsnis. Konstruojamas (9) charakteristinės lygties parametrizuotasis šaknų hodografas – harmoniškai linearizuotos sistemos charakteristinės lygties 1+ N(A)G(s) = 0 šaknų kontūrai. Akivaizdu, kad jų forma priklausys nuo funkcijos K2N2 (s) /[D(s) + K1N1(s)] polių ir nulių dislokacijos s plokštumoje.
Harmoniškai linearizuotos netiesinės sistemos valdymo kokybinių charakteristikų tyrimą, taikant šaknų hodografo metodą, galima atlikti naudojantis tiesinių sistemų analogiškų charakteristikų tyrimo metodika [1]:
- Netiesinės sistemos absoliučiojo stabilumo sąlygas nustato jos tiesioginio trakto stiprinimo ribinės reikšmės: jeigu sistema yra absoliučiai stabili esant maksimaliam (ribiniam) stiprinimui, tai ji išliks stabili esant bet kokiam stiprinimui.
- Netiesinės sistemos santykinio stabilumo (dinaminės) charakteristikos identifikuojamos tiriant jos dominuojančias (artimiausias kompleksinės s plokštumos menamajai ašiai s = jω ) charakteristines šaknis atitinkančių šaknų hodografo šakų dislokaciją: charakteristinių šaknų šiose šakose kitimo (migravimo) ribos, nustatytos esant tikėtinoms netiesinio elemento įėjimo signalo amplitudės reikšmėms, sąlygoja pereinamosios reakcijos charakteristikas: slopinimo koeficientą, svyravimo dažnį, slopimo dekrementą ir kt.
- Stabilūs arba nestabilūs ribiniai ciklai galimi tik tose netiesinėse sistemose, kurių šaknų hodografo šakos kerta s plokštumos menamąją ašį. Ribinio ciklo parametrai nustatomi iš šių susikirtimo taškų koordinačių: taškų ordinatės atitinka ribinio ciklo dažnį, o šaknų hodografo varijuojamo parametro reikšmė kirtimo taške – ribinio ciklo amplitudę. Galimo ribinio ciklo stabilumas nustatomas pagal charakteristinių šaknų migravimo (kirtimo taško aplinkoje) kryptį, esant mažiems amplitudės A pokyčiams ±ΔA .
Sistemos su statiniu netiesiškumu šaknų hodografas
Atskiru atveju, kai sistemos (1 pav.) netiesinio elemento charakteristika yra vienareikšmė ir simetrinė įėjimo signalo amplitudės A atžvilgiu (šie apribojimai tyrimuose leidžia aprėpti labai plačią praktinių netiesinių automatinių sistemų klasę), jo išėjimo signalo f (t) Fourier transformantė b(A) lygi nuliui. Tuo atveju netiesinio elemento ekvivalentinis stiprinimo koeficientas N(A) yra realus ir teigiamas, o sistemos (1 pav.) charakteristinė lygtis – tokia:
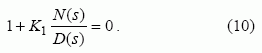
Šią charakteristinę lygtį atitinkančios harmoniškai linearizuotos sistemos (1 pav.) šaknų hodografas brėžiamas per visus s plokštumos taškus si (A) , tenkinančius šaknų hodografo kampų sąlygą (6), o nubrėžto hodografo atskirų taškų koordinatės nustatomos iš šaknų hodografo modulio sąlygos.
Šiuo atveju, netiesiškumą traktuojant kaip tiesinį kintamojo stiprinimo elementą, harmoniškai linearizuotos sistemos šaknų hodografui konstruoti galima panaudoti jos ekvivalentinę charakteristinę lygtį:
čia K = a(A) – varijuojamas parametras. Akivaizdu, kad šio šaknų hodografo forma sutaps su sistemos tiesinės dalies šaknų hodografo (sukonstruoto varijuojant jos tiesioginio trakto stiprinimui) forma. Tačiau netiesiškumo sąlygotas ir nuo amplitudės A priklausantis kintamas stiprinimas K priverčia charakteristines šaknis keisti padėtį (migruoti) jas atitinkančiose šaknų hodografo šakose. Šių šaknų kitimo ribos lengvai nustatomos iš netiesinių elementų analitinių arba grafinių modelių. Taigi harmoniškai linearizuotos sistemos (1 pav.) su vienareikšmiu netiesiškumu šaknų hodografas konstruojamas tokia seka:
1 žingsnis. Konstruojamas netiesinės sistemos tiesinės dalies šaknų hodografas (šio konstravimo elementarioms procedūroms beveik nereikia skaičiavimų [1]).
2 žingsnis. Remiantis sistemos netiesiškumo analitiniu arba grafiniu modeliu, nustatomas netiesinio elemento poveikis bendram sistemos tiesioginio trakto stiprinimui, tikėtinoms netiesinio elemento įėjimo signalo amplitudės A reikšmėms.
3 žingsnis. Naudojantis 2 žingsniu gautomis tiesioginio trakto kintamo stiprinimo reikšmėms, nustatomos šaknų hodografo šakų atskirų (bent jau ribinių) taškų koordinatės.
Pavyzdžiui, 2 paveiksle pavaizduotos automatinės sekimo sistemos, kurios netiesiškumą sąlygoja papildomo grįžtamojo ryšio grandinėje įtaisytas greičio jutiklis, šaknų hodografui konstruoti jos struktūrą patogu transformuoti (taikant struktūrinių schemų algebros taisykles [1]) į tipinę (1 pav.) tokia tiesinės dalies perdavimo funkcija:
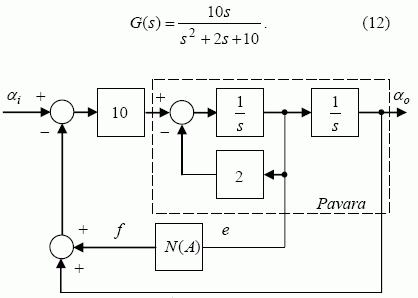
2 pav. Sekimo sistemos struktūrinė schema
Toliau transformuotajai sistemai galima tiesiogiai taikyti pateiktą šaknų hodografo konstravimo metodiką. Taigi, kaip išplaukia iš (10) formulės, automatinės sekimo sistemos (2 pav.) su harmoniškai linearizuotu greičio jutikliu ekvivalentinė charakteristinė lygtis yra tokia:
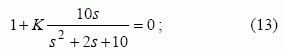
čia K = a(A) – varijuojamas parametras.
Siekiant nustatyti (13) charakteristinės lygties šaknų migravimo šaknų hodografo šakose ribas, kartu apibrėžti sekimo sistemos (2 pav.) pereinamosios reakcijos kokybinių charakteristikų kitimo sritį, nubraižome greičio jutiklio ekvivalentinio stiprinimo koeficiento N(A) (žr. 1 lentelę) priklausomybės nuo jo įėjimo signalo santykinės amplitudės A/ B grafiką, kai k = 1 (3 pav.) (šio jutiklio darbo tiesinėje charakteristikos dalyje parametro k ≠ 1 įtaką charakteristinių šaknų dislokacijai galima įvertinti sistemos tiesinės dalies modelyje).

1 lentelė. Greičio jutiklio modeliai[2]
Kaip matyti iš šio grafiko, greičio jutiklio ekvivalentinis kompleksinis stiprinimo koeficientas N(A) , net ir smarkiai keičiantis jo įėjimo signalo santykinei amplitudei A/ B , kinta palyginti nedideliame reikšmių diapazone. Pasinaudojus koeficiento N(A) priklausomybės nuo santykinės amplitudės A/B grafiku, konstruojamos sekimo sistemos su harmonikai linearizuotu greičio jutikliu charakteristinių šaknų hodografo fragmentas (graduojamas santykinės amplitudės dydžiu) (4 pav.), teikiantis išsamų vaizdą apie šios sistemos dinaminę elgseną.
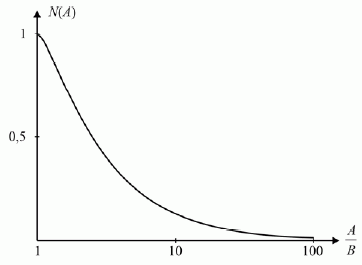
3 pav. Greičio jutiklio ekvivalentinis stiprinimo priklausomybės nuo santykinės amplitudės A/ B grafikas
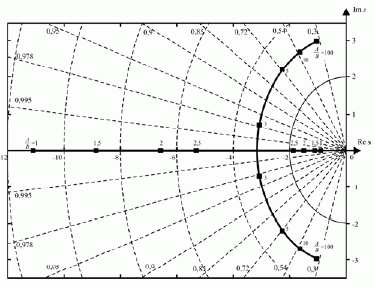
4 pav. Sekimo sistemos šaknų hodografo fragmentas
Išvados
- Harmoniškai linearizuotos netiesinės sistemos šaknų hodografas leidžia greitai ir paprastai gauti atsakymą apie jos elgseną – stabilumą, periodinio režimo ir pereinamosios reakcijos charakteristikas.
- Bendruoju atveju, kai sistemos netiesiškumas sukelia signalo fazės poslinkį, ekvivalentinės charakteristinės lygties šaknų migravimo s plokštumoje trajektorijos įgauna šaknų kontūrų formą.
- Atskiru atveju, kai netiesiškumo ekvivalentinis stiprinimo koeficientas yra realusis dydis, harmoniškai linearizuotos sistemos šaknų hodografas sutampa su sistemos tiesinės dalies šaknų hodografu, sukonstruotu varijuojant šios dalies stiprinimo koeficientą.
Literatūra
- Januševičius, V.S. Automatinis valdymas: teorija, uždaviniai, sprendimai. – Kaunas: Technologija, 2003.
- Техническая кибернетика/ Под. ред. В.В Солодовникова. – Москва: Машиностроение, 1969. – Kн. 3, ч. 1.
- Philips Ch.L., and Harbor R.D. Feedback Control Systems. – Englewood Cliffs, New Jersey: Prentice Hall, Inc., 2000.
A. Dervinienė, J. Daunoras, V. Januševičius. Netiesinių sistemų šaknų hodografo konstravimas // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2006. – Nr. 2(66), – P.75–77.


 Netiesinės automatinės sistemos elgseną, pereinant iš tam tikros pradinės būsenos į stabilios pusiausvyros būseną arba į stabilų priverstinį režimą, apibūdina jos pereinamoji reakcija. Šios reakcijos kokybei vertinti galima panaudoti sistemos santykinio stabilumo charakteristikas, kurios leidžia nustatyti pereinamosios reakcijos formą ir greitį, jos svyravimų dažnį, slopinimo laipsnį ir kt.
Netiesinės automatinės sistemos elgseną, pereinant iš tam tikros pradinės būsenos į stabilios pusiausvyros būseną arba į stabilų priverstinį režimą, apibūdina jos pereinamoji reakcija. Šios reakcijos kokybei vertinti galima panaudoti sistemos santykinio stabilumo charakteristikas, kurios leidžia nustatyti pereinamosios reakcijos formą ir greitį, jos svyravimų dažnį, slopinimo laipsnį ir kt.