Įvadas
Didžiausias įtampų matavimo tikslumas pasiekiamas taikant kompensacinius metodus [1, 2]. Trumpų elektrinių impulsų momentinių verčių kompensaciniams matavimams atlikti buvo sukurti specialūs elektroniniai vamzdžiai [3–5] su plokštelių pavidalo ir bėgančiosios bangos kreipimo sistemomis.
Momentinių įtampų verčių matuokliuose simetrinės bėgančiosios bangos kreipimo sistemos naudojamos nesimetriniu režimu. Į vieną lėtinimo ir kreipimo elektrodą nukreipiamas tiriamasis signalas, į kitą – kompensacinė įtampa. Tačiau tada kreipimo sistemoje susižadina nelyginė ir lyginė elektromagnetinės bangos. Dėl pastarosios bangos gali atsirasti papildomų tiriamojo signalo iškraipymų [2].
Siekiant išvengti šių iškraipymų, buvo pasiūlyta nesimetrinė bėgančiosios bangos kreipimo sistema su papildomu kompensaciniu elektrodu [3, 4].
J. V. Čaiko [6] pasiūlė alternatyvų sprendimą – panaudoti kreipimo sistemą, sudarytą iš dviejų spiralinių elektrodų, ir jos vienos spiralės (skirtos kompensacinei įtampai) vijas trumpai sujungti metalo sluoksniu, sudarytu ant keraminio spiralės laikiklio. Sprendimas buvo pagrįstas tuo, kad, veikiant kompensacinei įtampai ir įtampai, sužadinančiai sistema sklindančią elektromagnetinę bangą, vamzdžio jautrumas būna toks pat. Nors tokia kvazisimetrinė sistema buvo įdiegta plačiajuosčiame bėgančiosios bangos elektroniniame vamzdyje, nėra duomenų apie jos išsamesnius tyrimus. Konstatuota tik tai, kad sistemoje pasireiškia gana didelis slopinimas.
Šiame darbe, siekdami atskleisti reiškinius, lemiančius kvazisimetrinės spiralinės kreipimo sistemos savybes, sudarysime paprasčiausią sistemos modelį ir nagrinėsime trumpai sujungtų vijų įtaką sistemos lėtinimo koeficientui, įėjimo varžai ir slopinimui.
Kvazisimetrinės sistemos modelis
1 paveiksle pateiktas supaprastintas kvazisimetrinės spiralinės sistemos pjūvio vaizdas. Sistema sudaryta iš dviejų spiralių, vidinių ir išorinio ekranų ir keraminių laikiklių. Ant laikiklio 7 sudarytas metalo sluoksnis. Jis trumpai sujungia spiralės 2, kuri panaudota kaip kompensacinis elektrodas, vijas. Kaip ir [3, 7–9], kvazisimetrinės sistemos analizei taikysime daugialaidžių linijų metodą. Paprasčiausias kvazisimetrinės spiralinės sistemos modelis pavaizduotas 2 paveiksle. Jį sudaro dvieilės vienpakopės daugialaidės linijos atkarpa ir ekranai.
Daugialaidės linijos laidininkų potencialai ir srovės išreiškiami lygtimis [3]:
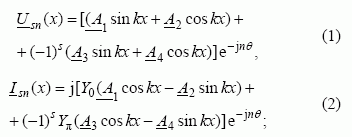
laidininko numeris, A – amplitudinis koeficientas, k – bangos skaičius, θ – gretimų daugialaidės linijos laidininkų įtampų ar srovių fazių skirtumas; Y0 (θ ) ir Yπ (θ ) – banginiai laidumai, kai gretimų daugialaidės linijos laidininkų įtampų ar srovių fazės skirtumas θ lygus 0 ir π .
Kai neįvertinama trumpai sujungtos vijos varža (R = 0), daugialaidės linijos atkarpa modeliuoja kvazisimetrinę sistemą, jeigu tenkinamos sąlygos:
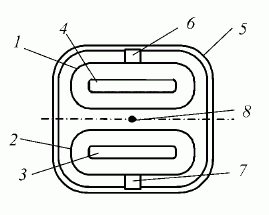
1 pav. Kvazisimetrinės spiralinės sistemos pjūvio vaizdas: 1, 2 – spiralių laidininkai, 3, 4 – vidiniai ekranai, 5 – išorinis ekranas, 6, 7 – spiralių laikikliai; 8 – elektronų pluoštas
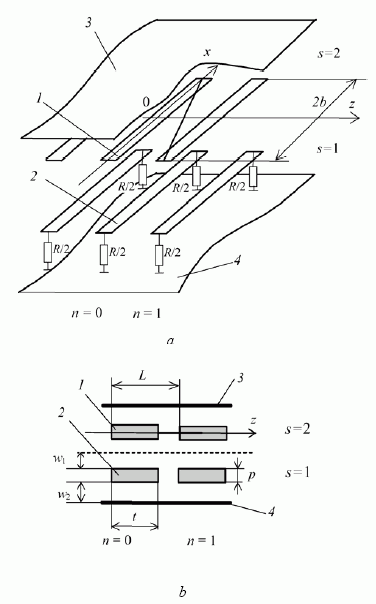
2 pav. Kvazisimetrinės sistemos modelis (a) ir daugialaidės linijos pjūvis (b):
1 – daugialaidės linijos laidininkas, modeliuojantis spiralės viją;
2 – daugialaidės linijos laidininkas, modeliuojantis trumpai sujungtą viją; 3, 4 – ekranai
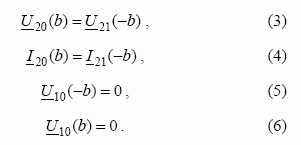
Tuomet įrašę į kraštinių sąlygų lygtis (3)–(6) įtampų ir srovių išraiškas (1), (2), spręsdami gautą lygčių sistemą, gauname du sprendinius:
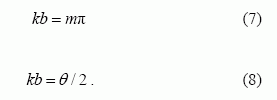
Remdamiesi (8), galime rasti lėtinimo koeficientą ir dažnį:
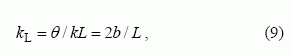
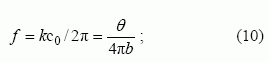
čia L – spiralės vijų ir daugialaidės linijos laidininkų žingsnis, c0 – šviesos greitis. Pagal (9) ir (10), kai neatsižvelgiama į vijų varžą, nagrinėjamos kvazisimetrinės spiralinės sistemos lėtinimo koeficientas pastovus.
(7) formulei galime suteikti tokį pavidalą:
čia m – sveikasis skaičius. Remiantis (7) ir (9), trumpai sujungtų vijų įtaka sistemos savybėms gali būti didžiausia, kai f = 0 ir esant rezonansiniams dažniams, kai vijos ilgyje telpa sveikasis pusbangių skaičius.
Sistemos įėjimo varžą galime rasti iš formulės
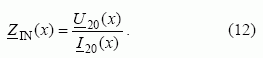
Bendruoju atveju ji priklauso nuo koordinatės x . Kai x = 0 ,
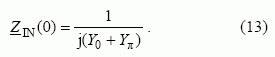
Atsižvelgiant į trumpai sujungtų vijų varžas ( R ≠ 0 ), turi būti tenkinamos sąlygos:
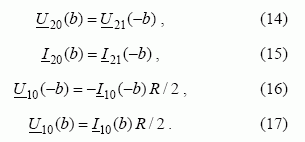
Įrašę į (14)–(17) lygtis įtampų ir srovių išraiškas ir pašalinę koeficientus A3 ir A4 , gauname lygčių sistemą:

Spręsdami šią lygčių sistemą, gauname sistemos dispersinę lygtį, kuriai galima suteikti tokį pavidalą:
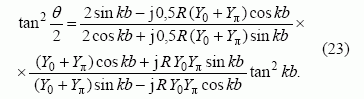
Pareikalavę, kad (18) lygčių sistemos determinantas būtų lygus nuliui, arba spręsdami (23) dispersinę lygtį, galime apskaičiuoti kampo θ realiosios (θr ) ir menamosios (θm) dedamųjų vertes, atitinkančias duotą arba pasirinktą bangos skaičiaus k vertę. Tada pagal θr galime apskaičiuoti lėtinimo koeficientą kL, o pagal θm – koeficientą α1, apibūdinantį slopinimą:
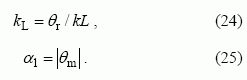
Žinodami koeficientą α1 ir atsižvelgdami į (1) ir (2), galime nustatyti, kaip keičiasi sistemos, sudarytos iš N vijų, įtampos perdavimo koeficiento modulis dėl nuostolių trumpai sujungtose vijose:
Žinodami koeficientų A1 ir A2 sąryšį ir taikydami (12) formulę galime rasti sistemos įėjimo varžą. Kai x = 0 , gauname:
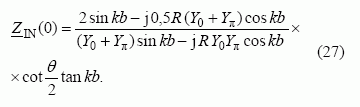
Alternatyvus slopinimo įvertinimo būdas
Koeficientą α1 taip pat galima rasti apskaičiavus sistemos periode (trumpai sujungtoje vijoje) prarandamą galią P1 ir sistemoje sklindančią galią P :
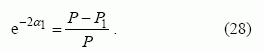
Pagal (28), kai P1 << P :

Trumpai sujungtoje vijoje prarandamą galią galime apskaičiuoti pagal formulę
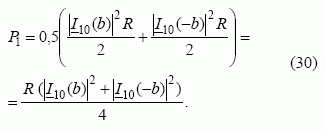
Sistemoje sklindanti galia gali būti nustatyta iš formulės
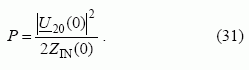
Įrašę (30) ir (31) lygtis į (29), gauname:
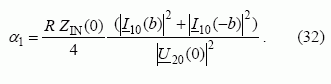
Kvazisimetrinės sistemos charakteristikos
Kaip minėjome anksčiau, trumpai sujungtų vijų įtaka turėtų būti didžiausia žemųjų dažnių srityje ir kai dažnis toks, kad trumpai sujungtos vijos ilgis yra pusės bangos ilgio kartotinis. Dažnis, atitinkantis žemiausią vijos rezonansinį dažnį, būtų už elektroninio vamzdžio praleidžiamųjų dažnių juostos ribų [3]. Be to, remiamės paprasčiausiu kvazisimetrinės sistemos modeliu (2 pav.), kuriame trumpai sujungtų vijų paskirstytosios varžos modeliuojamos sutelktosiomis varžomis. Atsižvelgdami į šias aplinkybes, toliau daugiausia dėmesio skirsime kvazisimetrinės sistemos savybėms žemųjų dažnių srityje. Trumpai sujungtos vijos varža priklauso nuo dažnio.
Atsižvelgiant į paviršinį efektą apskaičiuotos vijos varžos priklausomybės nuo dažnio pateiktos 3 paveiksle. Skaičiuojant laikyta, kad paviršinis efektas pradeda reikštis, kai srovės įsiskverbimo gylis tampa mažesnis už pusę vijos laidininko storio.
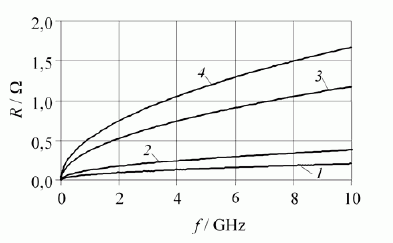
3 pav. Vijos varžos priklausomybės nuo dažnio ir medžiagos (1 – sidabras, 2 – molibdenas, 3 – konstantanas, 4 – nichromas), kai p = 0,2 mm, t = 1 mm, b = 7,5 mm
4 paveiksle, a, ir 5 paveiksle, a, pateiktos lėtinimo koeficiento kL ir įėjimo varžos modulio | ZIN (0) | priklausomybės nuo dažnio ir nuo trumpai sujungtos vijos medžiagos žemųjų dažnių ruože, 4 paveiksle, b, ir 5 paveiksle, b, – platesniame dažnių diapazone. Iš 4 ir 5 paveikslų matyti, kad tuo atveju, kai trumpai sujungtų vijų medžiaga idealiai laidi ( R = 0 ), lėtinimo koeficientas pastovus plačiame dažnių diapazone ir lygus konstrukciniam lėtinimo koeficientui kLk = 2b / L , o sistemos įėjimo varža žemųjų dažnių srityje pastovi. Didėjant dažniui, įėjimo varža mažėja pagal spiralinėms sistemoms būdingą dėsnį.
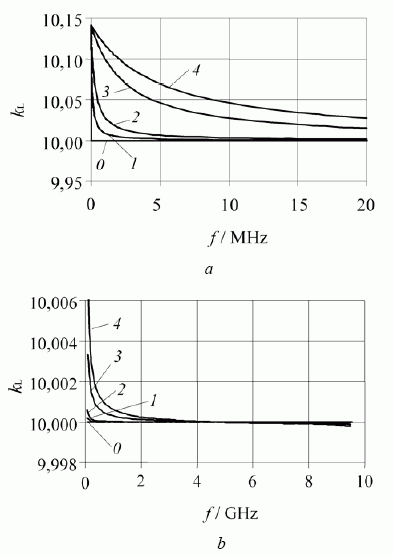
4 pav. Kvazisimetrinės sistemos lėtinimo koeficiento priklausomybės nuo dažnio žemųjų dažnių ruože (a) ir platesniame dažnių diapazone (b), kai L = 1,5 mm, t = 1 mm, p = 0,2 mm, b = 7,5 mm, w1 = 0,5 mm, w2 = 0,2 mm ir skirtingos trumpai sujungtų vijų medžiagos: 0 – idealiai laidi medžiaga (R = 0); 1 – sidabras; 2 – molibdenas; 3 – konstantanas; 4 – nichromas
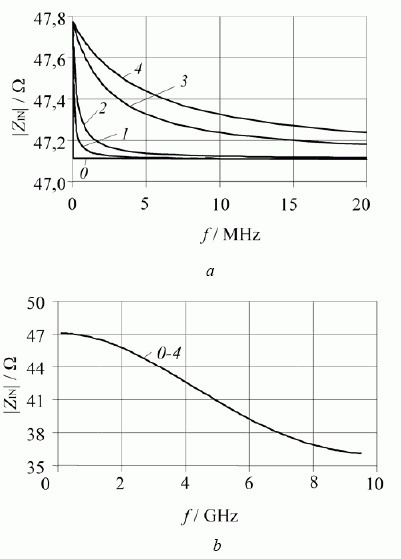
5 pav. Kvazisimetrinės sistemos įėjimo varžos priklausomybės nuo dažnio žemųjų dažnių ruože (a) ir platesniame dažnių diapazone (b), kai L = 1,5 mm, t = 1 mm, p = 0,2 mm, b = 7,5 mm, w1 = 0,5 mm, w2 = 0,2 mm ir skirtingos trumpai sujungtų vijų medžiagos: 0 – idealiai laidi medžiaga (R = 0); 1 – sidabras; 2 – molibdenas; 3 – konstantanas; 4 – nichromas
Kaip ir buvo tikėtasi, trumpai sujungtų vijų varžų įtaka didėja mažėjant dažniui. Kuo didesnė vijos varža, tuo didesnis lėtinimo koeficientas ir įėjimo varža žemųjų dažnių srityje ir platesnis dažnių ruožas, kuriame pasireiškia trumpai sujungtų vijų įtaka.
Didėjant dažniui, trumpai sujungtų vijų įtaka kvazisimetrinės sistemos lėtinimo koeficientui ir įėjimo varžai mažėja. Tai galima paaiškinti tuo, kad, didėjant dažniui, elektromagnetinis laukas telkiasi prie lėtinimo elektrodo ir kvazisimetrinėje sistemoje silpnėja elektromagnetinis ryšys tarp spiralės ir trumpai sujungtų vijų.
Pastarąją mintį patvirtina 6 paveikslo charakteristikos, apskaičiuotos, kai nuotolis 2w1 tarp kvazisimetrinės sistemos spiralės ir trumpai sujungtų vijų lygus 0,5 mm ir 1 mm. Akivaizdu, kad, padidinus nuotolį tarp spiralės ir trumpai sujungtų vijų, jų įtaka kvazisimetrinės sistemos lėtinimo koeficiento ir įėjimo varžos dažninėms charakteristikoms labai sumažėja.
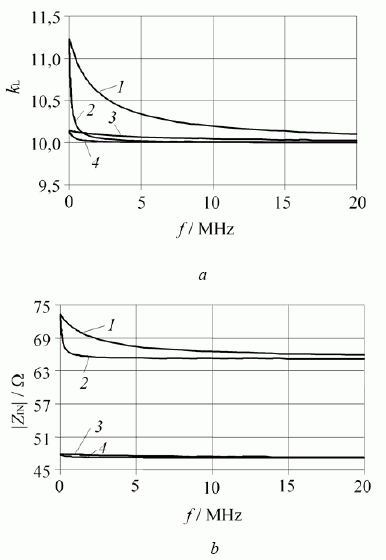
6 pav. Kvazisimetrinės sistemos lėtinimo koeficiento (a) ir įėjimo varžos (b) priklausomybės nuo dažnio žemųjų dažnių ruože, kai L = 1,5 mm, t = 1 mm, p = 0,2 mm, b = 7,5 mm: 1, 2 – w1 = 0,25 mm, w2 = 0,45 mm; 3, 4 – w1 = 0,5 mm, w2 = 0,2 mm; 1, 3 – nichromas; 2, 4 – molibdenas
7 paveiksle pavaizduotos perdavimo koeficiento modulio, gauto skaičiuojant koeficientą α1 dviem aptartais būdais, priklausomybės nuo dažnio. 7 paveikslo 1 – 4 kreivės, apskaičiuotos pagal įtampų ar srovių fazių skirtumo tarp gretimų vijų menamosios dalies modulį, 5 – 8 kreivės – pagal trumpai sujungtoje vijoje prarandamos galios ir sistemoje sklindančios galios santykį. Iš 7 paveikslo kreivių matyti, kad taikant abu būdus gaunami tapatūs rezultatai.
Pagal 7 paveikslą dėl nuostolių trumpai sujungtose vijose sistemos amplitudės dažninė charakteristika gaunama netolygi. Kuo didesnės trumpai sujungtų vijų varžos, tuo jų įtaka didesnė – pasireiškia didesnis slopinimas kvazisimetrinėje sistemoje.
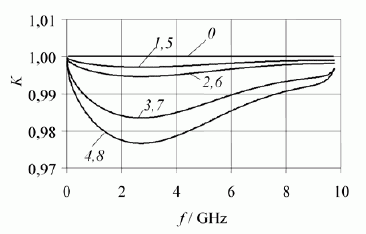
7 pav. Kvazisimetrinės lėtinimo sistemos perdavimo koeficiento modulio priklausomybės nuo dažnio, kai N = 60, L = 1,5 mm, t = 1 mm, p = 0,2 mm, b = 7,5 mm, w1 = 0,5 mm, w2 = 0,2 mm: 0 – neįvertinus trumpai sujungtos vijos varžos (R = 0); 1, 5 – sidabras; 2, 6 – molibdenas; 3, 7 – konstantanas ; 4, 8 – nichromas
Atsižvelgiant į bėgančiosios bangos elektroninių vamzdžių charakteristikų priklausomybes nuo elektrodinaminių kreipimo sistemų charakteristikų [3, 7–9], verta pažymėti, kad daugiausia įtakos elektroninio vamzdžio su kvazisimetrine kreipimo sistema charakteristikoms gali turėti kreipimo sistemos banginės varžos kitimas žemųjų dažnių srityje ir slopinimas dėl įneštinių nuostolių, pasireiškiančių trumpai sujungtose vijose.
Atsižvelgdami tik į paviršinį efektą gavome, kad kvazisimetrinės sistemos įėjimo varžos pokytis žemųjų dažnių srityje gali siekti 1,5 % (5 pav., a). Slopinimas kreipimo sistemoje dėl įneštinės varžos nėra didelis (7 pav.). Kreipimo sistemos amplitudės dažninės charakteristikos netolygumas vien tik dėl trumpai sujungtų vijų varžų, apskaičiuotų atsižvelgiant į paviršinį efektą, gali būti kelių decibelo dalių eilės.
Autoriai dėkoja doc. dr. V. Urbanavičiui už naudingas diskusijas, pastabas ir pasiūlymus.
Išvados
Kvazisimetrinę spiralinę lėtinimo ir kreipimo sistemą galima modeliuoti daugialaide linija. Dėl trumpai sujungtų vijų kinta kvazisimetrinės spiralinės kreipimo sistemos lėtinimo koeficientas ir sistemos įėjimo varža žemųjų dažnių srityje. Didėjant dažniui trumpai sujungtų vijų įtaka mažėja, nes silpnėja elektromagnetinis ryšys tarp spiralės ir trumpai sujungtų vijų.
Dėl nuostolių trumpai sujungtose vijose padidėja slopinimas kvazisimetrinėje sistemoje. Trumpai sujungtų vijų įtaka slopinimui tuo didesnė, kuo didesnės vijų varžos ir kuo stipresnis elektromagnetinis ryšys tarp spiralės ir trumpai sujungtų vijų.
Trumpai sujungtų vijų įtaką slopinimui galima įvertinti dviem būdais – pagal įtampų ar srovių fazių skirtumo tarp gretimų vijų menamąją dalį arba pagal trumpai sujungtose vijose prarandamos galios ir sistemoje sklindančios galios santykį.
Literatūra
- Seilius A. Elektroninių matavimų metrologijos pagrindai. – Vilnius: Technika, 2003. – 271 p.
- Bell D. A. Electronic instrumentation and measurements. – New Jersey: Prentice Hall, 1994. – 451 p.
- Штарас С., Вайнорис З., Мартавичюс Р., Скудутис Ю., Станкунас Й. Широкополосные тракты осциллографических электронно-лучевых трубок бегущей волны. – Вильнюс: Техника, 1993. – 360 с.
- Вайнорис З. А., Мартавичюс Р. Л., Шкунов В. А., Штарас С. С. Отклоняющая система бегущей волны. Описание изобретения к авторскому свидетельству 449391.
- Павлов С. И., Топчиев Г. М. Электронные нуль- индикаторы для компенсационных измерений импульсных напряжений // ПТЭ. – 1969. – № 6. – C. 103– 106.
- Чайко Ю. В, Губанова Л. И, Михеева В. В. СВЧ осциллографическая трубка с полосой пропускания 5 ГГц // Электронная промышленость. – 1971. – № 4. – С. 49.
- Вайнорис З., Кирвайтис Р., Штарас С. Электродина- мические задерживающие и отклоняющие системы. – Вильнюс: Мокслас, 1986. – 266 с.
- Štaras S., Skudutis J. Traveling-wave deflecting systems // Software for Electrical Engineering Analysis and Design. – Boston, Southampton: WITPRESS, 1999. – P. 23–32.
- Staras S. Simulation and properties of the twined helical deflecting structure // IEEE Trans. Electron Devices, vol. 52, no. 6, p. 1222–1225, June 2005.
Štaras S., Burokas T. Kvazisimetrinės spiralinės kreipimo sistemos modelis ir savybės // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2006. – Nr. 2(66), – P. 68–73


 Momentinių įtampų verčių matuokliuose simetrinės bėgančiosios bangos kreipimo sistemos naudojamos nesimetriniu režimu. Į vieną lėtinimo ir kreipimo elektrodą nukreipiamas tiriamasis signalas, į kitą – kompensacinė įtampa. Tačiau tada kreipimo sistemoje susižadina nelyginė ir lyginė elektromagnetinės bangos. Dėl pastarosios bangos gali atsirasti papildomų tiriamojo signalo iškraipymų.
Momentinių įtampų verčių matuokliuose simetrinės bėgančiosios bangos kreipimo sistemos naudojamos nesimetriniu režimu. Į vieną lėtinimo ir kreipimo elektrodą nukreipiamas tiriamasis signalas, į kitą – kompensacinė įtampa. Tačiau tada kreipimo sistemoje susižadina nelyginė ir lyginė elektromagnetinės bangos. Dėl pastarosios bangos gali atsirasti papildomų tiriamojo signalo iškraipymų.