Elektromechaninių energijos keitiklių nestacionariųjų procesų tyrimai

Įvadas

Naujoms mechatroninėms sistemoms ir gamybos įrenginiams reikalingos elektros pavaros, veikiančios paleidimo, darbo, greičio reguliavimo ir stabilizavimo, tiksliojo stabdymo ir pozicionavimo režimais. Todėl jas kuriant plačiai naudojami ne tiktai rotaciniai, bet ir specialieji elektros varikliai, kurių veikimas pagrįstas slenkamuoju magnetiniu lauku. Pastarajai grupei priskiriami lankiniai, būgniniai ir plokštieji elektros varikliai, varikliai su diskiniu rotoriumi ar segmentiniu statoriumi, taip pat varikliai, turintys du arba daugiau diskinių ar tuščiavidurių rotorių. Kadangi šis elementas automatinėse pavarose naudojamas ir variklio, ir stabdymo režimais, todėl čia jis nagrinėjamas kaip elektromechaninis energijos keitiklis (EMK) [1].

Automatinėse pavarose su specialiaisiais EMK dažniausiai realizuojami nestacionarieji stabdymo režimai: dinaminis, rekuperacinis, vienfazis, kondensatorinis stabdymas, stabdymas priešiniu jungimu, pulsuojančiąja srove ir invertorinis (dažninis) stabdymas. Stabdymo metu EMK judančioje dalyje, o kai kuriais atvejais ir induktoriuje vyksta gana sudėtingi tarpusavyje susiję elektromagnetiniai ir elektromechaniniai nestacionarieji procesai [2].

Literatūros šaltinių analizė rodo [3, 4], kad kol kas nėra pakankamai tvirtai moksliškai pagristų metodikų, kurios leistų tirti EMK nestacionariuosius stabdymo procesus ir skaičiuoti jų dinamines charakteristikas, atsižvelgiant į daugelį tokių keitiklių specifinių savybių.

Dėl atviros magnetinės grandinės ir aktyviosios zonos baigtinio ilgio atsirandančio išilginio kraštų efekto specialieji EMK pasižymi vidine magnetine ir elektrine asimetrija. Tokios asimetrijos neturi įprastinės konstrukcijos rotaciniai elektros energijos keitikliai. Dėl to žinomi EMK matematiniai modeliai ir analizės metodai netinka tokiems nesimetriniams keitikliams tirti. Todėl būtina ne tik ieškoti naujų modelių, bet ir juos moksliškai pagrįsti.

Šio darbo tikslas – apžvelgti tiesiaeigių variklių ir pavarų tyrimo mokslines publikacijas, sudaryti dinaminį modelį, atsižvelgiant į stabdymo srovės ir greičio kitimą.

EMK nestacionarieji procesai

Nestacionarieji procesai – visuma elektromagnetinių ir elektromechaninių reiškinių, susijusių ne tik su keitiklio maitinimo įtampos, srovės, apkrovos ir antrinio elemento greičio kitimu stabdymo metu (neigiamu pagreičiu), bet ir su elektromagnetinio lauko kraštų efektais. Sąvoka „nestacionarieji procesai“ platesnė už klasikinėje keitiklių teorijoje vartojamą sąvoką „pereinamieji procesai (vyksmai)“ ir apima platesnį keitiklyje vykstančių fizikinių reiškinių spektrą.

Nestacionarieji procesai būdingi ir kintamosios srovės kolektoriniams EMK. Praktikoje paplitę vienfaziai mažos galios kolektoriniai elektros varikliai, kuriuose negali būti įrengtos įprastinės komutacijos gerinimo priemonės – papildomieji poliai ir kompensavimo apvija [5, 6]. Tokiuose keitikliuose dėl nekompensuotos elektrovaros vyksta netiesiniai inkaro srovės komutavimo procesai, kurie turi įtakos ne tik keitiklio charakteristikoms, patikimumui, bet ir kibirkščiavimo bei radijo trikdžių intensyvumui.

Literatūros šaltinių apžvalga rodo, kad visus nestacionariųjų sistemų analizės metodus galima suskirstyti į tris pagrindines grupes [7–9]:

a) metodai, kuriais tiriami pereinamieji procesai ir laikinės sistemų charakteristikos;

b) metodai, pagrįsti funkciniais kintamųjų pakeitimais; c) skaitiniai metodai, pagrįsti specialiosiomis kompiuterinėmis programomis.

Moksliniuose tyrimuose, norint gauti analizinius sprendinius, dažniau taikomi antrosios grupės metodai, pagrįsti Laplaso, Furjė, Melino, Hankelio, Uolšo ir kitais funkciniais kintamųjų pakeitimais. Sistemoms su lėtai kintančiais parametrais tirti taikomi Furjė ir nuosekliųjų priartėjimų metodai. Impulsinių nestacionariųjų sistemų analizei taikomas diskretinis Laplaso (Z pakeitimas) ir kiti panašūs pakeitimai. Tačiau šie metodai dažniausiai taikomi nestacionariųjų sistemų su sudėtingais elektriniais kontūrais ir grandinėmis analizei. Jie nepritaikyti keitiklių su nestacionariaisiais magnetiniais laukais dinaminėms charakteristikoms tirti.

Kuriant ir diegiant naujas technologijas su specialiaisiais EMK, ypač svarbi yra nestacionariųjų stabdymo režimų, visų pirma magnetinio lauko ir dinaminių charakteristikų, tyrimo problema. Kita problema, susijusi su nepakankamai išanalizuotais stabdymo režimais, yra ta, kad be moksliškai pagrįstų metodikų neįmanoma kurti optimalių automatinio Todėl šios tarpusavyje susijusios problemos turi būti sprendžiamos kompleksiškai, atsižvelgiant į naujausių technologijų reikalavimus. Šiuo požiūriu nemaži rezervai sukaupti moksliniuose kolektyvuose, vykdančiuose šios srities tiriamuosius darbus.

Nestacionariųjų stabdymo režimų, magnetinių laukų ir dinaminių charakteristikų analizė, įvertinant kraštų efektus bei antrinio elemento greičio kitimą, yra sudėtinga mokslinė problema. Ją sėkmingai gali spręsti tik nemažas kolektyvas, dirbdamas pakankamai ilgą laiką. Jau daugiau kaip 30 metų tiesiaeigių pavarų, jų valdymo bei stabdymo sistemų mokslo tiriamieji darbai atliekami Vilniaus Gedimino technikos universiteto (anksčiau Vilniaus inžinerinio statybos instituto) Automatikos katedroje.

Elektromagnetinių procesų tiesiaeigiuose varikliuose ir pavarose tyrimai

Specialiųjų EMK nestacionariųjų stabdymo procesų tyrimo galimybės atsirado tada, kai buvo sukurti ir apibendrinti magnetohidrodinaminių mašinų (MHD) ir tiesiaeigių asinchroninių variklių (TAV) teoriniai pagrindai ir išnagrinėti stacionarieji jų darbo režimai. Intensyvūs šių mašinų tyrimai buvo pradėti po Antrojo pasaulinio karo, kai prireikė sukurti skystųjų metalų siurblius branduolinės energetikos tikslams ir naujas greitaeigio transporto sistemas. Susiformavo nemaža mokslinių kolektyvų, kurie sėkmingai sprendė ne tik teorines šios technikos srities problemas, bet ir praktinio naudojimo klausimus. Išsamūs teoriniai ir eksperimentiniai MHD mašinų ir TAV tyrimai buvo atlikti tuometiniuose Talino, Rygos, Kijevo, Permės, Novočerkasko politechnikos institutuose, Novosibirsko elektrotechnikos institute, Latvijos MA Fizikos institute, Rygos magnetinės hidrodinamikos SKB ir kitose organizacijose.

Mūsų šalyje tiesiaeigių elektros mašinų tyrimai buvo pradėti 1970 m., kai tuometiniame Vilniaus inžineriniame statybos institute (dabar Vilniaus Gedimino technikos universitetas, Automatikos katedra) buvo įkurta Žinybinė tiesiaeigių elektros variklių laboratorija, kurios mokslinis vadovas buvo doc. techn. m. kand. (dabar prof. habil. dr.) V. Česonis. Šioje laboratorijoje, kuri veikė iki 1976 m., atlikti tyrimai ir parengtos mokslinės publikacijos apžvelgtos straipsniuose [10, 11]. Čia parodyta, kad mokslo tiriamieji darbai, pradėti Žinybinėje laboratorijoje, toliau tęsiami Vilniaus Gedimino technikos universiteto Automatikos katedroje ir dabar sudaro pagrindinę šios katedros mokslinių tyrimų kryptį. Straipsnyje [11] teigiama, kad Lietuvoje susikūrė pajėgi savarankiška tiesiaeigių elektros variklių ir pavarų mokslo mokykla.

Nuo 1975 iki 1994 m. tiesiaeigių variklių ir pavarų teoriniai ir eksperimentiniai tyrimai buvo buvo atliekami ir Sąjunginio mažųjų elektros mašinų mokslinio tyrimo instituto Vilniaus skyriuje, kuris 1986 m. buvo reorganizuotas į Sąjunginio elektros mašinų gamybos ir technologijos mokslinio tyrimo instituto Vilniaus filialą. Specifinės TAV savybės, kurių neturi rotaciniai asinchroniniai varikliai, įgalina kurti specialiąsias automatines sistemas įvairioms technikos sritims. Ilgainiui susiformavo nauja mokslinio tyrimo kryptis – specialiųjų automatinių ir mechatroninių sistemų kūrimas ir jų tyrimas sistemotechnikos metodais. Šios srities tyrimų rezultatai apibendrinti habilitaciniuose darbuose [12, 13] ir monografijose [14, 15].

Pastaraisiais metais tyrinėtojų dėmesys sutelktas į dar palyginti mažai nagrinėtų tiesiaeigių elektromechaninių ir mechatroninių sistemų problemų sprendimą. Klaipėdos universiteto prof. S. Kudarausko anglų kalba parašytoje monografijoje [16] apžvelgti mūsų šalyje ir užsienyje atliekami švytuojamojo judesio EMK tyrimai. Monografijoje pateikta išsami netradicinių ir specialios paskirties EMK klasifikacija pagal konstrukcijos ypatumus ir judesio pobūdį. Daug dėmesio skirta elektros mašinų ir EMK terminologijai.

EMK stabdymo režimų tyrimai

Kuriant šiuolaikinėms technologijoms naujas mechatronines sistemas su specialiaisiais EMK, reikia atsižvelgti į tai, kad tenka dažnai tų sistemų judamąsias dalis stabdyti. Stabdymo jėgą galima gauti naudojant mechaninius, hidraulinius, pneumatinius ir elektromagnetinius įtaisus arba perjungiant pavaros variklį į elektrinio stabdymo režimą. Pastarasis būdas praktikoje plačiausiai taikomas, nes tuo atveju EMK naudojamas efektyviausiai. Stabdymo teorijos ir charakteristikų skaičiavimo klausimams nagrinėti skirta nemažai mokslinių darbų, kuriuose buvo naudojami matematiniai modeliai, besiskiriantys elektromagnetinių stabdymo procesų idealizavimo laipsniu ir skaičiavimo tikslumu [17].

Tiesiaeigių EMK stabdymo režimų tyrimai atliekami ir mūsų šalyje. Jau minėtoje Žinybinėje laboratorijoje kaip atskira mokslo ir technikos problema susiformavo TAV stabdymas. Jos tyrimui vadovavo prof. A. Smilgevičius [18].

Mokslinių publikacijų analizė rodo, kad tiesiaeigių variklių ir pavarų stabdymo režimai nėra plačiai ištirti, nors tokie režimai yra neatskiriama automatinių ir mechatroninių sistemų darbo ciklo dalis. Šioje srityje dar mažai tirti nestacionarieji stabdymo procesai, kai kinta induktoriaus srovė ir antrinio elemento greitis, ir beveik netirti TAV su trumpa antrine dalimi stabdymo procesai.

EMK nestacionariųjų procesų matematinis modelis Visų nestacionariųjų stabdymo režimų analizei gali būti panaudotas pagrindinis ir bendriausias EMK teorinis skaičiuojamasis modelis, parodytas 1 pav. [2, 3].

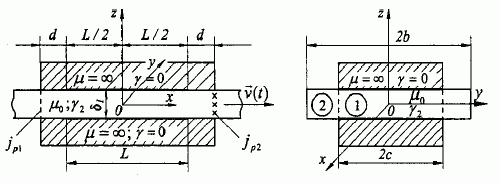
1 pav. EMK stabdymo režimų teorinis skaičiuojamasis modelis: L – aktyviosios (sužadintos) zonos ilgis; 2c ir 2b – aktyviosios zonos ir antrinio elemento plotis; d – papildomų magnetolaidžių ilgis; μ ir γ – magnetolaidžių magnetinė skvarba ir elektrinis laidis; μ₀ ir γ₂ – antrinio elemento magnetinė skvarba ir elektrinis laidis; v (t ) – antrinio elemento greičio vektorius; δ₁ – oro tarpo tarp magnetolaidžių dydis; j_p1 ir j_p2 – papildomi stabdymo srovės paviršinio tankio sluoksniai.

Stačiakampėje koordinačių sistemoje x y z stabdymo srovės tūrinis tankis vaizduojamas erdviniu vektoriumi, kuris aprašomas ne realiomis, o kompleksinėmis funkcijomis – fazoriais. Kondensatorinio stabdymo atveju aktyviosios zonos ilgyje L sukuriama srovės tūrinio tankio banga, kurios kompleksinė amplitudė išreiškiama šiuo fazoriumi:

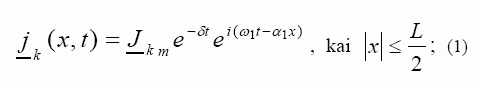
čia J_km – srovės tūrinio tankio amplitudė; δ ir ω₁ – stabdymo srovės silpimo koeficientas ir jos kampinis dažnis; i = √−1 ; α₁ =π/τ – srovės tūrinio tankio erdvinis dažnis; τ – srovės tūrinio tankio pusbangės ilgis arba induktoriaus poliaus žingsnis.

Vienfazio stabdymo atveju aktyviojoje zonoje L pulsuojanti kintamosios srovės tūrinio tankio banga skaidoma į dvi priešingų krypčių bėgančiąsias bangas:

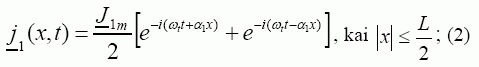
čia J_dm – dinaminio stabdymo srovės tankio amplitudė. Turint anksčiau pateiktus pradinius duomenis, magnetinio lauko uždavinys sprendžiamas spektriniu metodu, pagal kurį neperiodinei laiko funkcijai (1) ir neperiodinėms koordinatės x funkcijoms (1) – (3) taikomi integralieji Furjė pakeitimai [5]. Spektrinio metodo fizikinė prasmė ta, kad 1 pav. pavaizduotas EMK modelis pakeičiamas be galo dideliu skaičiumi elementariųjų modelių, kurių aktyviosios zonos yra begalinių matmenų.

Tokiuose modeliuose išilginio ir skersinio kraštų efektų nėra, todėl Maksvelo lygčių sprendiniai užrašomi harmoninių funkcijų pavidalu. Elementariajame modelyje galioja superpozicijos principas, todėl suminio magnetinio lauko stipris susideda iš dviejų dedamųjų:

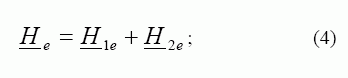
čia H_e1 , H_e2 – pirminio ir antrinio magnetinio lauko stiprio elementariosios dedamosios kompleksinė amplitudė.

Išsprendus Maksvelo lygčių sistemą vienmačiam laukui, H_e1 skaičiuoti gauta tokia diferencialinė lygtis:

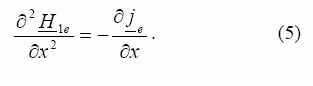
Sprendžiant Maksvelo lygtis, antrinio elemento greičio kitimas stabdymo metu įvertinamas nuosekliųjų intervalų metodu, pagal kurį kiek norima mažame laiko intervale greitis yra tiesinė laiko funkcija:

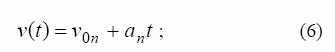
čia v_0n – greitis n-ojo intervalo pradžioje; a_n = const – neigiamas pagreitis, laikomas pastoviu n-ojo intervalo ribose.

Greičio aproksimacija tiesinėmis atkarpomis parodyta 2 pav.

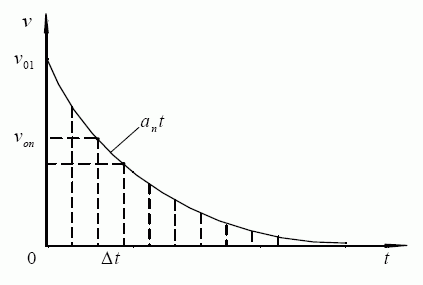
2 pav. Greičio pereinamojo proceso aproksimacija tiesinėmis atkarpomis

Pirmasis straipsnis apie 2 pav. parodytą pagreičio įvertinimą TAV pereinamųjų procesų skaičiavimuose buvo paskelbtas dar 1979 metais [19].

EMK dinaminėms mechaninėms charakteristikoms skaičiuoti Maksvelo lygtyse daromas toks integravimo kintamojo pakeitimas:

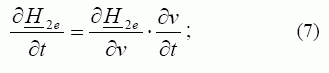
čia 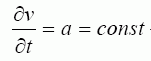antrinio elemento neigiamas pagreitis stabdymo metu laikomas pastoviu.

Antriniame elemente indukuoto magnetinio lauko elementariosios dedamosios kompleksinei amplitudei skaičiuoti gauta tokia diferencialinių lygčių sistema [2, 3]:

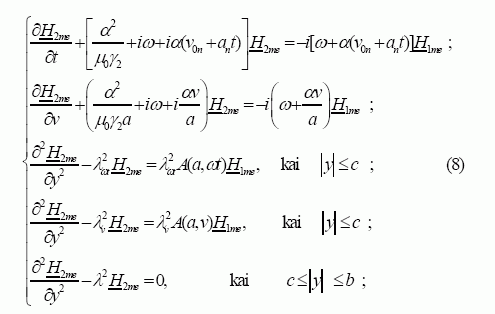
čia H_1me – atitinkamo stabdymo režimo pirminio magnetinio lauko stiprio elementariosios dedamosios kompleksinė amplitudė;

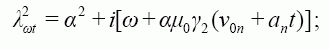
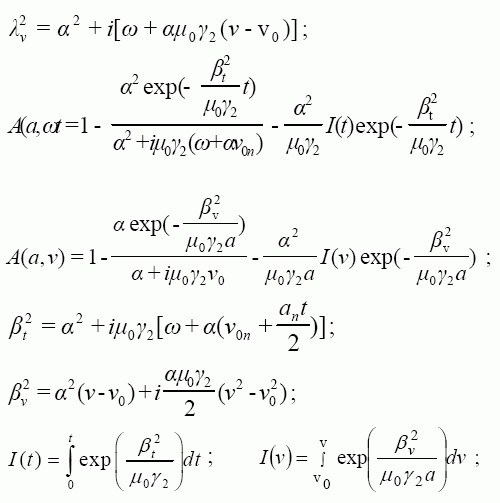
λ² – apibendrintoji kompleksinė funkcija, vietoj kurios skaičiuojant pereinamuosius procesus imama λ²_ωt vertė, o skaičiuojant dinamines charakteristikas, imama λ²_v vertė.

Pirmosios dvi (8) sistemos lygtys yra tiesinės diferencialinės lygtys su kintamaisiais koeficientais, kurios negali būti išspręstos elementariosiomis matematinėmis funkcijomis. Jų sprendimo rezultatuose egzistuoja integralai I(t) ir I(v), priklausantys Frenelio tipo integralams [3].

Pateikto modelio privalumas yra tas, kad, panaudojus specialiąsias matematines funkcijas – Frenelio tipo integralus, (8) sistemos lygtis galima išspręsti analitiškai.

Išvados

Paskelbtoje mokslinėje literatūroje yra nemaža darbų, skirtų specialiųjų EMK stabdymo problemoms tirti. Tačiau daugelyje iš jų nagrinėjami tik nusistovėję (stacionarieji) stabdymo režimai. Pagal literatūroje žinomas išraiškas galima skaičiuoti ir tirti tik statines keitiklio charakteristikas ir mechaninius pereinamuosius procesus, nes šiuo atveju keitiklio būsena stabdymo metu visiškai atitinka nusistovėjusio režimo sąlygas.

[11] parodyta, kad Vilniuje susikūrė pajėgi ir savarankiška tiesiaeigių elektros variklių ir pavarų mokslo mokykla. Iš variklinio režimo ir tiesiaeigių pavarų teorijos Vilniaus mokykloje apginti trys habilitaciniai darbai ir septynios daktaro disertacijos, o iš tiesiaeigių variklių ir pavarų stabdymo režimų šioje mokykloje apgintas tik vienas habilitacinis darbas ir trys daktaro disertacijos.

Tai rodo, kad tiesiaeigių variklių ir pavarų stabdymo režimai dar nėra pakankamai ištirti, nors jie yra neatskiriama mechatroninių sistemų darbo ciklo dalis. Nestacionariųjų procesų analizei sudarytas teorinis skaičiuojamasis modelis ir gautos EMK stabdymo režimų dinamikos diferencialinės lygtys, kuriose įvertintas stabdymo srovės ir antrinio elemento greičio kitimas ir išilginio bei skersinio kraštų efektų tarpusavio sąveika.

Literatūra

Boldea I., Nasar A. Linear electric actuators and generators // IEEE Int. Conf. on Electric Machines and Drives. Conference record. – 1997. – P. MA1/1.1–Ma1/1.5
Darulienė O., Karaliūnas B. Mathematical Model of Non- Stationary Braking Processes of Electromechanical Power Converters // Proc. of 11-th Int. Conf. On Power Electronics and Motion Control. EPE-PEMC 2004. – Riga, Latvia. – 2004. – Vol. 3. – P. 3-415 – 3-419.
Karaliūnas B. Tiesiaeigio variklio stabdymo režimų matematinis modelis // Elektronika ir elektrotechnika. – Kaunas: Technologija. – 1997. – Nr. 2(11). – P. 30–35.
Karaliūnas B. Specialiųjų elektros variklių stabdymo režimų pereinamieji procesai // Elektronika ir elektrotechnika. – Kaunas: Technologija. – 1998. – Nr. 2(15). – P. 68–73.
Puternicki P. Silniki komutatorowe malej mocy. – Warszawa: Instytut Elektrotechniki. – 2000. – 371 p.
Karaliūnas B. Vienfaziai kolektoriniai elektros varikliai ir jų skaičiavimo metodai // Elektronika ir elektrotechnika. – Kaunas: Technologija. – 2000. – Nr. 4(27). – P. 17–21.
Пухов Г. Е. Дифференциальные спектры и модели. – Киев: Наукова Думка. – 1990. – 184 с.
Береговенко Г. Я., Пухов Г. Е. Численные операторные методы решения дифференциальных уравнений и анализа динамических систем. – Киев: Наукова Думка. – 1993. – 384 с.
Ефименко Е. И. Новые методы анализа электрических машин переменного тока и их приложения. – Москва: Энергоатомиздат. – 1993. – 280 с.
Smilgevičius A., Poška A., Rinkevičienė R., Teišerskas Č. Specialiosios automatinės sistemos su tiesiaeigėmis elektros pavaromis // Elektronika ir elektrotechnika. – Kaunas: Technologija. – 2001. – Nr. 5(34). – P.76–87.
Smilgevičius A. Tiesiaeigių elektros variklių tyrimai Lietuvoje // Elektronika ir elektrotechnika. – Kaunas: Technologija. – 2004. – Nr. 1(50). – P. 22–27.
Poška A. J. Specialiosios automatinės sistemos: Habil. darbas. – Vilnius: Technika. – 1995. – 203 p.
Rinkevičienė R. Tiesiaeigės mechatroninės sistemos: Habil. darbas. – Vilnius: Technika. – 2003. – 136 p.
Poška A., Teišerskas Č. Automatinės sistemos su tiesiaeigėmis elektros pavaromis. – Vilnius: Technika. – 1993. – 174 p.
Poška A., Rinkevičienė R. Teisiaeigių elektros pavarų skaičiavimo ir valdymo algoritmai. – Vilnius: Technika. – 1997. – 232 p.
Kudarauskas S. Introduction to Oscillating Electrical Machines. – Klaipėda, Lithuania. – 2004. – 184 p.
Smilgevičius A. Tiesiaeigių asinchroninių variklių stabdymo tyrimai Lietuvoje // Elektronika ir elektrotechnika. – Kaunas: Technologija. – 2005. – Nr. 1(57). – P. 42–47.
Smilgevičius A. Tiesiaeigių asinchroninių variklių stabdymas. – Vilnius: Technika. – 1992. – 56 p.
Каралюнас Б. С., Смильгявичюс А. Ю. Об учете ускорения в расчетах переходных процессов линейных асинхронных двигателей // Электротехника: Темат. сб. научн. тр. вузов Лит. ССР. –1979. – T. 5 (14). – C. 75–79.

B. Karaliūnas. Elektromechaninių energijos keitiklių nestacionariųjų procesų tyrimai // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2006. – Nr. 1(65). – P. 68–72.