Vėlinimų valdymas modeliuojant sistemas Petri tinklais

Įvadas

Valdymo sistemoms projektuoti ir analizuoti, ypač jeigu jos didelės, netiesinės ar stochastinės, reikia specialių programinių priemonių, kurios šiuos procesus palengvintų, padarytų lengviau suvokiamus ir paspartintų darbą. Dažnai tenka naudoti tokių sistemų modelius, todėl modeliavimo priemonės, programų paketai darosi vis svarbesni. Diskretinėms sistemoms modeliuoti plačiai naudojami Petri tinklai [1], kuriais lengva modeliuoti konkuruojančius procesus. Be to, jeigu į konkurencijos sąlygas įeina atsitiktiniai dydžiai, procesai Petri tinkluose yra Markovo procesai ir savo ruožtu gali būti modeliuojami Markovo grandinėmis [2], diskrečiomis ar tolydžiomis, o šios analizuojamos taikant Petri tinklų modifikaciją – stochastinius Petri tinklus [3]. Yra žinoma nemaža darbų skirtų šiems klausimams nagrinėti. Tačiau universalių priemonių nėra. Todėl vis dažniau atsiranda uždavinių, sistemų, kurioms analizuoti nepakanka žinomų Petri tinklų. Kartais siūlomi sprendimai yra gana netikėti, pavyzdžiui, [4] darbe siūlomi Petri tinklai, kuriuose žetono turinys, atributai gali būti Petri subtinklai.

Globalusis laikas ir vėlinimai

Bendruoju atveju laikas Petri tinkluose yra globalus, nuo vartotojo nepriklausantis kintamasis. Jis gali būti siejamas su pozicijomis, pereigomis ar žetonais [5]. Modeliuojant valdymo sistemas, natūralu laiką susieti su pereigomis, nes pereigos yra tie tinklo elementai, kurių aplinkoje priimami „sprendimai“. Procesai, kuriems atlikti reikalinga laiko trukmė, susiejami su pereigomis ir proceso trukmę atitinka pereigos vėlinimas, t. y. laiko tarp pereigos inicijavimo ir atsidarymo intervalas. Pereigos veikimas susideda iš dviejų etapų – inicijavimo metu tikrinamos konkurencinės sąlygos ir, jeigu jos tenkinamos, pereiga inicijuojama, o pereigoms, turinčioms vėlinimą, jis yra paleidžiamas; antrasis etapas – pereigos atsidarymas, t. y. išėjimo šakų žetonų generavimas, o pereigoms, turinčioms vėlinimą, žetonų generavimas galimas tik pasibaigus vėlinimui.

Kita vertus, vėlinimų buvimas atsispindi sistemos laike, nes procesų, susijusių su pereigomis, neturinčiomis vėlinimo, trukmė yra nulinė. 1 pav. pavaizduota Petri tinklo su dviem kartu inicijuojamomis pereigomis, turinčiomis vėlinimus, pereigų atsidarymo statistikos histograma. Globalusis sistemos laikas keičiamas tik tada, kai tinkle nebėra inicijuotinų pereigų be vėlinimo [6]. Taigi pereigų vėlinimai yra valdymo sistemos modelio sinchronizavimo priemonė. Sistemos sinchronizavimo, veikimo tvarkos ir trukmės, valdymas neišvengiamai veda prie vėlinimų pereigose valdymo, nes visi realūs procesai yra laiko funkcijos.

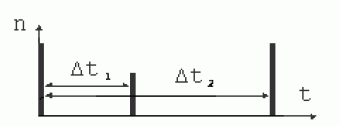
1 pav. Sinchronizavimo histograma: n – atsidariusių pereigų skaičius, Δt₁ ir Δt₂ – dviejų pereigų vėlinimai

Kai sistemoje vykstančių procesų trukmės yra žinomos – žinomi ir juos modeliuojančių pereigų vėlinimai, tačiau toks atvejis retai pasitaiko net ir determinuotose valdymo sistemose.

Procesų pobūdis, o kartu ir trukmė, dažnai priklauso nuo daugelio parametrų. Todėl paranku turėti galimybę pereigų vėlinimus skaičiuoti dinamiškai, t. y. pereigos inicijavimo metu. Tuo tikslu siūloma pereigos atributus papildyti pereigos vėlinimo reiškiniu [7 ]. Šiame reiškinyje gali būti naudojamos deklaruotos konstantos ir pereigos įėjimo šakų konstruktorių apibrėžti kintamieji.

Vėlinimo trigeris

Valdymo sistemose vykstantys procesai gali būti nutraukiami. Tipiškas pavyzdys yra lanksti gamybos sistema su mobiliaisiais robotais. Robotų judėjimas – trajektorijos, kryptys, trukmės – čia nėra iš anksto žinomas ir, atsirandant konfliktams su kitais robotais, reikia kai kuriuos iš jų stabdyti ar keisti judėjimo kryptis bei greičius. Galimų konfliktų skaičius tokiose sistemose yra milžiniškas, todėl jų Petri tinklo struktūroje aprioriškai įvertinti neįmanoma.

Taigi reikalingos atskirų veiksmų trukmės gali pasikeisti proceso metu ir modeliuojant tokią sistemą būtina turėti galimybę dinamiškai valdyti vėlinimo trukmę jau po pereigos inicijavimo.

Autoriai programų pakete CENTAURUS-C [7] siūlo du vėlinimo trukmės valdymo variantus. Vienas iš jų pavadintas „vėlinimo trigeriu“ traktuoja pereigą su vėlinimu kaip trigerį – inicijuojant neaktyvią pereigą paleidžiamas vėlinimo mechanizmas, tačiau jeigu pereiga aktyvi, t. y. turi veikiantį vėlinimą, pakartotinis pereigos inicijavimas vėlinimą nutraukia. Šiam mechanizmui sukurti būtina papildoma informacija apie pereigą – aktyvi ar ne, vėlinimas baigėsi „natūraliai“ ar buvo nutrauktas, todėl pereigos aplinkoje prieinami du sistemoje iš anksto deklaruoti kintamieji – $deltat ir $dtrem. Pirmasis, pasibaigus vėlinimui, apibūdina faktinę vėlinimo trukmę, o antasis – vėlinimo likutį, t. y. laiko intervalą, likusį iki nebaigto, nutraukto, pradžios metu apskaičiuoto vėlinimo pabaigos. Jeigu vėlinimas baigiasi „natūraliai“, t. y. nėra nutraukiamas, $dtrem = 0, kitaip $dtrem > 0. Be to, norint valdyti vėlinimą, būtina žinoti, ar pereiga aktyvi. Tam tikslui įvesta standartinė funkcija engaged (), kurios rezultatas yra loginis (BOOL) ir lygus true, jeigu pereiga turi aktyvų vėlinimą. Ši funkcija leidžiama tik įėjimo šakų ir kontrolės reiškiniuose. Tokio pereigos vėlinimo valdymo pavyzdys parodytas 2 pav.

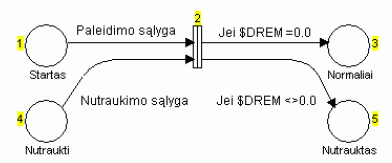
2 pav. Vėlinimo trigerio valdymas

2-oji pereiga inicijuojama, vėlinimo skaitiklis paleidžiamas, į 1-ąją poziciją įrašius loginį (bool) žetoną true. Vėlinimas nutraukiamas įrašant analogišką žetoną 4-ojoje pozicijoje. Šakose, jungiančiose šias pozicijas su 2-ąja pereiga reiškiniuose esanti funkcija engaged() leidžia nepriklausomai inicijuoti pereigą ir nutraukti vėlinimą. Išėjimo šakų reiškiniuose naudojamas kintamasis $dtrem, kurio vertė leidžia atskirti nutrauktą vėlinimą nuo normaliai pasibaigusio. Toks vėlinimo valdymas turi vieną esminį trūkumą – pereigos įėjimo šakų reiškiniai yra sąlyginiai ir juose, laikantis sintaksės, negalima naudoti kintamųjų priskyrimo rinkinių (konstrukcijų), antraip gali likti neinicijuotų kintamųjų. Kitaip tariant, žetonų, esančių 1 ar 4 pozicijose, atributai negali būti perduoti pereigai ir negali būti naudojami vėlinimo trukmei skaičiuoti.

Vėlinimo nutraukimo sąlyga

Kitas siūlomas vėlinimo valdymo būdas – dinamiškai tikrinti aktyvaus vėlinimo pabaigos sąlygą. Tuo tikslu pereigos atributai papildomi specialiu vėlinimo pabaigos kontrolės reiškiniu, kuris skaičiuojamas dinamiškai, t. y. jo reikšmė tikrinama po kiekvieno vėlinimo dekremento. Šio reiškinio rezultatas yra loginis (bool) ir vėlinmas nutraukiamas, kai reiškinio rezultatas yra false. Kad toks valdymas būtų efektyvus, t. y. vėlinimo pabaigos reiškinio vertė keistųsi, turi keistis šiame reiškinyje dalyvaujantys kintamieji. Lokalių kintamųjų pereigos inicijavimo metu įgytos vertes viso vėlinimo metu išlieka nekintamos, todėl būtina naudoti globalius kintamuosius. Globaliojo kintamojo vertė visada turi būti apibrėžta, todėl globalusis kintamasis inicijuojamas jau jį deklaruojant. Deklaravimo sintaksė yra tokia:

global var name = expression;

čia name – globaliojo kintamojo vardas, expression – reiškinys, sudarytas iš deklaruotų žinomų dydžių, kurio rezultatas nusako kintamojo spalvą ir reikšmę.

Paslėptieji ryšiai ir globaliųjų kintamųjų kontrolė

Naudoti globaliuosius kintamuosius gana rizikinga, nes taip galima sukurti paslėptus ryšius. 3 pav. parodytas vizualiai nesuformuotas, Petri tinklų sintaksėje draudžiamas paslėptasis ryšys tarp dviejų šakų reiškinių.

Vienas globalusis kintamasis – laikas ($time) jau naudojamas Petri tinkluose. Tačiau laiko reikšmė gali būti tik skaitoma ir šitaip išvengiama paslėptųjų ryšių. Siūloma leisti globaliuosius simbolius tik vėlinimo pradinės vertės ir vėlinimo kontrolės reiškinyje. Taigi globalieji kintamieji turėtų įtakos tik Petri tinklo sinchronizacijai. Visais kitais atvejais jie būtų traktuojami kaip ir lokalieji. Šitoks rezultatas pasiekiamas laikantis tokių taisyklių:

1. pereigos aplinkos reiškiniuose gali būti naudojami tik įėjimo šakų konstruktorių inicijuoti kintamieji (įskaitant ir globaliuosius);
2. vėlinimo inicijavimo ir vėlinimo pabaigos kontrolės reiškiniuose leidžiama naudoti įėjimo šakų konstruktorių inicijuotus ir paskelbtus globaliais kintamuosius.

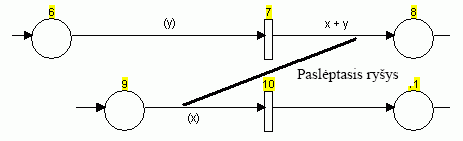
3 pav. Neleistinas paslėptasis ryšys per globalųjį kintamąjį x

Modeliavimo pavyzdys

Transportavimo robotas yra ypatingas tuo, kad, judėdamas į paskirties tašką, jis gali būti vienos iš dviejų būsenų. Viena iš jų, kai robotas, keisdamas savo padėtį, ką nors transportuoja, kita – kai, keisdamas savo padėtį, jis nieko netransportuoja. Pirmuoju atveju robotui turi būti leidžiama užbaigti jau pradėtą operaciją, o antruoju atveju roboto vykdoma operacija, bet kuriuo momentu gali būti pakeista kita operacija.

Realiam robotui judant iš vieno taško į kitą, jo kelią seka kelio jutiklis, tačiau jei norėsime tokį procesą modeliuoti, susidursime su ta problema, kad roboto nueito kelio nepavyksta modeliuoti tiesiogiai, o apie nueitą kelią galime spręsti iš kitų netiesioginių parametrų. Jei robotas juda pastoviu greičiu, vienas iš tokių parametrų yra roboto sugaištas laikas. Tokios situacijos modelis pateiktas 4 paveiksle. Čia roboto eiga yra modeliuojama 156 perdavos vėlinimo trukme, kuri bendruoju atveju yra apskaičiuojama pagal įvairias sąlygas, taip pat ir priklausomai nuo roboto judėjimo greičio.

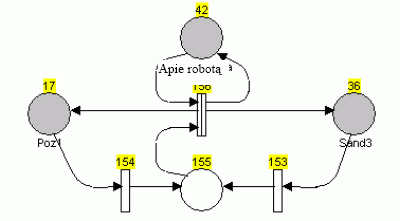
4 pav. Roboto eigos modeliavimas tarp taškų Poz1 ir Sand3

Jeigu yra galimybė pertraukti jau vykdomą operaciją ir ją pakeisti nauja, kyla problema, kad reikia nutraukti pereigos 156 funkcionavimą, t. y. nutraukti modeliuojamą vėlinimą, o po to spręsti problemą nurodant naujos užduoties parametrus. Vienu atveju robotas galės tęsti savo eigą, bet jau su nauja užduotimi, kitu atveju robotas turi keisti judėjimo kryptį priešinga. Pirmuoju atveju jis turės užbaigti 156 pereigos likusį vėlinimą, o antruoju atveju, pakeitęs judesio kryptį, grįžti atgal, sugaišdamas tiek laiko, kiek buvo jo sugaišta judant pradine kryptimi.

Kaip minėta, pereigos aplinkoje prieinami du sistemos kintamieji $deltat ir $dtrem. Pirmasis kintamasis $deltat, pasibaigus vėlinimui, apibūdina įvykdytą vėlinimo trukmę, o antrasis kintamasis $dtrem apibūdina vėlinimo likutį, t. y. laiko intervalą, likusį iki starto metu apskaičiuoto vėlinimo pabaigos. Jei vėlinimas yra nutraukiamas, $dtrem vertė nėra nulinė.

4 paveiksle pateiktas modelis, norint valdyti aprašytą vėlinimo trukmę, transformuojamas į modelį, pateiktą 5 paveiksle.

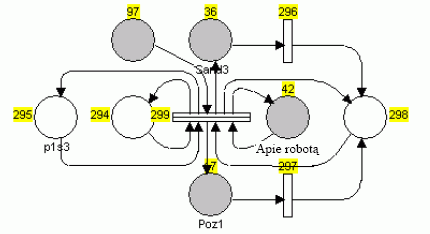
5 pav. Roboto eigos modelis tarp taškų Poz1 ir Sand3, kai 299 pereigos vėlinimas gali būti nutrauktas, o po to vykdoma nauja užduotis

Šakos 299-36 ir 299-17 persiunčia roboto žetoną viena ar kita kryptimi, priklausomai nuo roboto judėjimo krypties ir tik tuomet, kai vėlinimas yra visiškai pasibaigęs, t. y. $DTrem=0.0. Vėlinimo trukmė pereigoje 299 yra organizuojama taip:

if ti = 0.0 then atstumas/greitis else ti;

čia ti – kintamasis, nusakantis buvusią $DTrem vertę, kuri cirkuliuoja kontūru 299-294.

Pozicija 295 ypatinga tuo, kad joje yra susiejami atstumo parametrai deklaracijose su pozicijos vardu. Todėl analogiški kitų kelio atkarpų modeliai tampa parametriškai nepriklausomi, o jų vertę nustato konkretus pozicijos vardas. Naudojantis šia pozicija apskaičiuojamas vėlinimo parametras atstumas/greitis.

Vėlinimas valdomas globaliuoju kintamuoju keisti ir, jei vykdoma operacija turi būti pakeista kita operacija, jam yra priskiriama vertė true. Tuo pat metu žetonui 42 pereigoje priskiriami naujos užduoties robotui parametrai, kurių vienas yra ir judėjimo kryptis. Vėlinimas valdomas funkcija Wrinkle, kurios naudojimas aprašytas 299 pereigoje

if keisti then Wrinkle(keisti) else false .

Funkcija Wrinkle nutraukiamas 299 pereigos vėlinimas, fiksuojant kintamųjų $deltat ir $dtrem vertes. Jei kintamasis $dtrem yra nelygus nuliui, pereigai 299 priskiriamas naujas vėlinimas

if $DTrem <> 0.0 then
if (kurlink=k) then $DTrem else $DeltaT
else 0.0 .

Jei kintamieji kurlink ir k yra lygūs, judėjimas tęsiamas buvusia kryptimi, o jei ne, judėjimas keičiamas į judesį kryptimi, priešinga buvusiai.

6 paveiksle parodyta, kaip funkcionuoja robotas, kai vėlinimas nevaldomas, 7 paveiksle – kai vėlinimas valdomas.

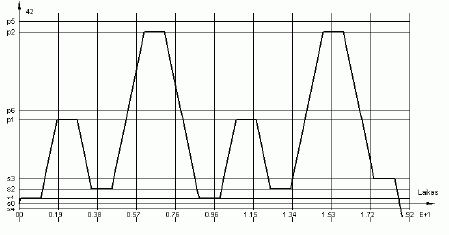
6 pav. Roboto, aptarnaujančio lanksčią liniją, funkcionavimo fragmentas, kai vėlinimas nevaldomas

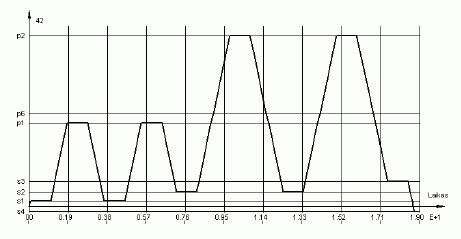
7 pav. Roboto, aptarnaujančio lanksčią liniją, funkcionavimo fragmentas, kai vėlinimas valdomas

Lanksti linija funkcionuoja taip: robotas vykdo aukščiausio prioriteto pertraukimą, t. y. paima ruošinį iš sandėlio s1 ir transportuoja jį staklėms į poziciją p1, padeda jį ir eina vykdyti kitos užduoties, t. y. robotas vyksta į sandėlį s2, kad iš ten paimtų ruošinį ir aptarnautų antras stakles. Kadangi valdymo sistema užduoties nekeičia, kai ji yra vykdoma, tai nors robotui tuščiomis judant į sandėlį s2 vėl atsiranda poreikis aptarnauti poziciją p1, nes ruošinys iš pozicijos p1 paimamas staklių ir pradedamas jo apdirbimas, o sistemai yra generuojamas atitinkamas pertraukimas, tačiau jau vykdomas pertraukimas nėra keičiamas. 6 paveiksle matome, kad pozicijos aptarnaujamos eilės tvarka: p1, p2, p1, p2.

Kaip pakinta funkcionavimas, kai vėlinimai valdomi, aiškiai parodyta 7 paveiksle. Lanksti linija dabar funkcionuoja taip: robotas vykdo aukščiausio prioriteto pertraukimą, t. y. paima ruošinį iš sandėlio s1 ir transportuoja jį staklėms į poziciją p1, padeda jį ir eina vykdyti kitos užduoties, t. y. robotas vyksta į sandėlį s2, kad iš ten paimtų ruošinį ir aptarnautų antras stakles. Tuo metu ruošinys iš pozicijos p1 paimamas staklių ir pradedamas jo apdirbimas, o sistemai yra generuojamas atitinkamas aukštesnio prioriteto pertraukimas. Kadangi robotas, judėdamas į sandėlį s2, nieko netransportuoja, jo užduotis keičiama svarbesne, t. y. robotas vėl eina aptarnauti pirmosios pozicijos. Užduotis pakeičiama intervale p1 – s2, ir pakeitus užduotį robotas toliau juda ta pačia kryptimi, bet jau iki sandėlio s1. 7 paveiksle matome, kad pozicijos aptarnaujamos eilės tvarka: p1, p1, p2, p2.

Išvados

Modeliuojant valdymo sistemas Petri tinklais, racionalu valdyti pereigų vėlinimų trukmę.

Vėlinimus galima valdyti keliais būdais, bet racionaliausia įvesti į pereigų atributus specialų vėlinimo trukmės kontrolės reiškinį su globaliais kintamaisiais.

Literatūra

1. Richard Molner. Performance Modelling with Deterministic and Stochastic Petri Nets// The American Mathematical Monthly.–1998–105, 9. –885p.
2. Pham D.T, Parhi D. R. Navigation of multiple mobile robots using neural network and a Petri Net model // Robotica, 2003.–Vol.21. –P.79–93.
3. Bartkevičius S.K., Mačerauskas V., Šarkauskas K. Spalvotųjų Petri tinklų taikymas valdymo sistemoms modeliuoti // Elektronika ir elektrotechnika.–2003.– Nr. 4(16).–P. 7–11.
4. Horton G., Kulkarni V.G., Nicol D.M, Trivedi K.S., Fluid stocastic Petri nets: Theory, applications and solution techniques // European Journal of Operational Research.– 1998.–No. 105.–P. 184–201.
5. Cabac L., Kohler M. Relating Higher Order Reference Nets and Well-Formed Nets // Fifth Workshop on Practical Use of Colourd Petri Nets and the CPN Tools.-2004 october 8-11, University of Aarhus, Denmark.
6. Falko Bause, Pieter S. Kritzinger. Stochastic Petri Nets. Vieweg Verlag 2, 2002.–218 p.
7. Bartkevicius S., Macerauskas V., Sarkauskas K. Simulation of hybrid control systems using open Petri nets. Industrial Simulation 2003 : 1st International Industrial Simulation Conference.-ISC'2003, June 9–11, 2003.–Valencia, Spain.–P. 131–135.
8. Hermanns H., Herzog U., and Katoen J.P. Process Algebra for Performance Evaluation // Theoretical Computer Science.–2002.–Vol. 247 (1–2).–P. 43–87.

S. Bartkevičius, J. Daunoras, R. Kragnys, K. Šarkauskas. Vėlinimų valdymas modeliuojant sistemas Petri tinklais // Kaunas: Technologija, 2006. – Nr. 1(65). – P. 16–19.