Skysčio lygio valdymas taikant „fuzzy“ logiką

Įvadas

Skysčio lygiui valdyti plačiai naudojami atvirojo kontūro ir proporcingieji integraliniai (PI) reguliatoriai. Tačiau dėl skysčio lygio valdymo sistemų netiesiškumo bei parametrų nepastovumo (skiriasi talpyklos konfigūracija, ištakos ertmės skersmuo ir t. t.) čia gaunami gana vidutiniški valdymo kokybės rodikliai [1]. Todėl svarbu rasti naujų būdų skysčio lygiui valdyti. Tokioms ir panašioms netiesinėms sistemoms valdyti šiuo metu vis plačiau taikoma „fuzzy“ logika.

„Fuzzy“ logika

„Fuzzy“ aibių teorija apibendrina klasikinę loginių aibių teoriją. Čia objekto priklausomybės laipsnis aibėje nėra apibrėžtas sveikaisiais skaičiais 0 (objektas aibei nepriklauso) ir 1 (objektas aibei priklauso), bet gali būti bet kuris skaičius iš intervalo [0,1]. „Fuzzy“ logikos sistemas (FLS) apibūdina „fuzzy“ aibės (angl. fuzzy sets) ir „fuzzy“ ryšiai (angl. fuzzy relations). FLS yra taisyklėmis pagrįstos sistemos, naudojamos netiesiniam ryšiui tarp sistemos įėjimo ir išėjimo erdvių sudaryti (1 pav.).

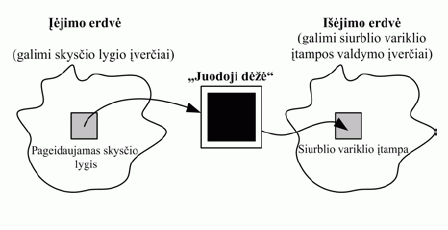
1 pav. Ryšys tarp įėjimo ir išėjimo erdvių

Vienas svarbiausių „fuzzy“ logikos elementų yra lingvistiniai kintamieji, kurie yra sudaromi iš viena kitą dengiančių „fuzzy“ aibių, fizikine prasme apibūdinančių tą kintamąjį [2].

Tarp įėjimo ir išėjimo yra vadinamoji „juodoji dėžė“, kurioje ir sprendžiama problema. „Juodojoje dėžėje“ gali būti ir „fuzzy“ logikos, tiesinės, ekspertinės sistemos, neuroniniai tinklai, diferencialinės lygtys, daugiamatės lentelės ir t. t. [3].

„Fuzzy“ aibė – tai išplėstoji klasikinė aibė. Jei X yra įėjimo erdvė, o x – tos erdvės elementai, tai „fuzzy“ aibė A erdvėje X:

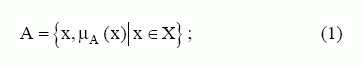
čia μ_A – x priklausomybės aibei A funkcija (2 pav.).

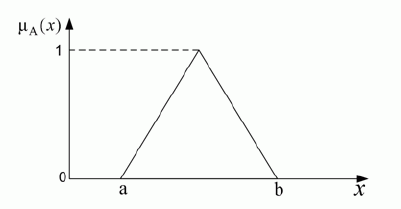
2 pav. Priklausomybės aibei A funkcija

Įėjimo erdvės intervale [a,b] priklausomybės funkcija įgauna nenulinę vertę. 2 pav. pateikta priklausomybės funkcija yra trikampio formos. Tačiau ji gali būti trapecijos, Gauso skirstinio, varpo ar kitos formos. Lingvistinės jei..., tuomet... taisyklės yra naudojamos sąlyginėms formuluotėms sudaryti (pvz., jei x yra A, tuomet y yra B), kur A ir B yra lingvistiniai įverčiai, o x priklauso „fuzzy“ aibei X, y – „fuzzy“ aibei Y. Pirmoji taisyklės „jei x yra A, tuomet y yra B“ dalis vadinama prielaida, antroji – padariniu arba išvada.

Pvz., jei x (skysčio lygis) yra A (per žemas), tuomet y (siurblio variklio įtampa) yra B (didelė).

Prielaida skysčio lygis yra per žemas gali būti klaidinga, iš dalies teisinga arba visiškai teisinga. Priklausomai nuo to, priklausomybės aibei skysčio lygis yra per žemas funkcija įgyja skaitinę vertę nuo 0 iki 1. Jei prielaida yra klaidinga, priklausomybės funkcija įgauna nulinę vertę, jei visiškai teisinga – vienetinę vertę, jei prielaida yra teisinga tik iš dalies, priklausomybės funkcijos vertė yra iš intervalo [0,1]. Išvada, kad siurblio variklio įtampa yra didelė, yra nauja „fuzzy“ aibė. Sprendžiant uždavinį, dažnai reikia sudaryti keletą taisyklių, turinčių daugiau negu vieną prielaidą. Tokiu atveju visos taisyklės vertinamos lygiagrečiai, taikomi atitinkami loginiai operatoriai, kiekvienos taisyklės išėjimo aibės sudedamos, ir iš gautosios randamas konkretus skaičius – uždavinio sprendinys.

„Fuzzy“ logikos reguliatorius

Pagrindinė valdymo, taikant „fuzzy“ logiką, teigiamybė – galimybė valdyti sudėtingas sistemas, panaudojant žmogiškąją patirtį ir protą, nedalyvaujant žmogui. Čia a priori žinios panaudotos sukurti tokiam reguliatoriui, kuris valdo sistemą taip, kaip pats geriausias operatorius [5].

„Fuzzy“ logikos reguliatoriaus modelis yra panašus į kitus tradicinių reguliatorių modelius, tačiau išsiskiria iš visų kitų savo įėjimo ir išėjimo parametrų aprašymo struktūra, taip pat ir pačiu įėjimų transformavimo į išėjimus (sprendinio priėmimo) procesu [2].

3 pav. pateikta proceso valdymo sistema ir „fuzzy“ logikos reguliatoriaus architektūros modelis.

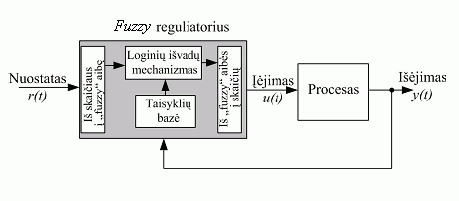
3 pav. Proceso valdymo sistema ir „fuzzy“ logikos reguliatoriaus architektūros modelis [4]

Reguliatorių sudaro šios dalys:

Taisyklių bazė (angl. rule base) yra „jei..., tuomet...“ (angl. If...–Then...) taisyklių rinkinys. Taisyklės pagrįstos ekspertų patarimais, kaip tinkamai valdyti sistemą. Loginių išvadų mechanizmas (angl. inference mechanism) išrenka, kurios taisyklės yra tinkamiausios, ir jas pritaiko.

„Fazifikavimo“ sąsaja (angl. fuzzification interface) reguliatoriaus įėjimo signalus pakeičia taip, kad loginių išvadų mechanizmas galėtų suaktyvinti ir pritaikyti logines taisykles.

„Defazifikavimo“ sąsaja (angl. defuzzification interface) keičia logines išvadas į valdomojo proceso įėjimo signalą.

Valdomasis objektas

Valdomasis objektas – nevienalytės formos talpykla. Skystis į ją patenka varomas siurblio, kurį valdo nuolatinės srovės variklis su nuolatiniais magnetais. Skystis laisvai išteka pro kiaurymę talpyklos apačioje (4 pav.). Talpyklos matematinis modelis:

čia v_s – skysčio srovės greitis, h – skysčio lygis, g – laisvojo kryčio pagreitis.

čia q_out – per sekundę ištekančio skysčio tūris, a – ištakos kiaurymės skerspjūvis.

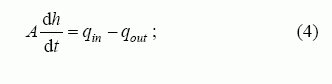
čia A – skysčio talpyklos skerspjūvis, q_in – per sekundę įtekančio skysčio tūris (skysčio debitas):

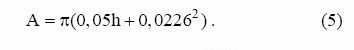
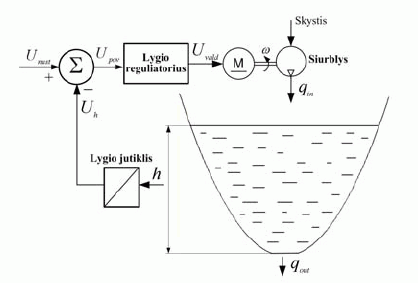
4 pav. Skysčio lygio valdymo sistemos funkcinė schema

Skysčio lygiui valdyti naudojamo PI reguliatoriaus matematinis modelis:

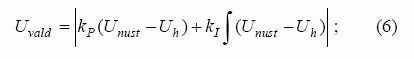
čia k_P, k_I – reguliatoriaus proporcingojo ir integralinio valdymo koeficientai, U_nust – skysčio lygio nuostatas, U_h – tikrojo skysčio lygio signalas.

Imitacijos rezultatai

Taikant paketo MATLAB priedą „Simulink“, atlikta skysčio lygio valdymo, panaudojant PI ir „fuzzy“ logikos reguliatorius, procesų imitacija. Imitacijos metu nustatyti šie sistemos parametrai: ištakos kiaurymės skerspjūvio plotas – 16 cm⁻², pradinis skysčio lygis – 0,8 m, siekiamas skysčio lygis – 0,2 m.

Skysčio lygio valdymo, panaudojant PI reguliatorių, imitacijos rezultatai pateikti 5 ir 6 pav. Iš 5 pav. matyti, kad, reguliuojant skystį žemyn, gaunamas didelis dinaminis nuokrypis. Nuokrypis nežymiai mažėja, didėjant proporcingosios reguliatoriaus dalies koeficientui k_P. Iš 6 pav. matyti, kad, didinant reguliatoriaus integralinės dalies koeficientą k_I, galima sumažinti pereinamojo proceso trukmę.

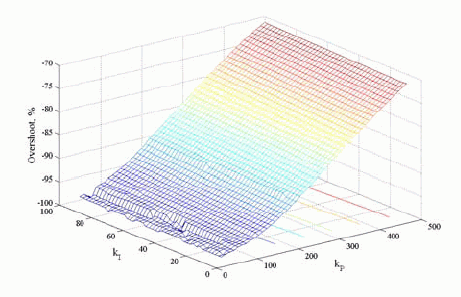
5 pav. Skysčio lygio valdymo dinaminio nuokrypio priklausomybė nuo PI reguliatoriaus koeficientų k_P ir k_I

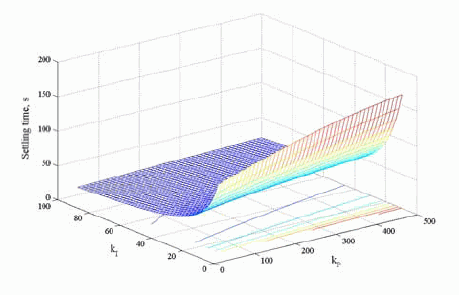
6 pav. Skysčio lygio valdymo pereinamojo proceso trukmės priklausomybė nuo PI reguliatoriaus koeficientų k_P ir k_I

Pateikti paveikslai įrodo, kad skysčio lygiui valdyti PI reguliatorius nėra labai efektyvus.

Valdymui pagerinti, projektuojamas „fuzzy“ reguliatorius, turintis du įėjimus (skysčio lygio paklaidos ir jos kitimo greičio signalus) ir vieną išėjimą – siurblio variklio įtampos keitimo greičio signalą.

Reguliatoriaus darbas aprašomas taikant šias lingvistines taisykles:

1. Jei valdymo paklaida yra neigiama, tuomet siurblio variklio įtampą reikia labai sumažinti.
2. Jei valdymo paklaida yra artima nuliui ir paklaidos kitimo greitis yra teigiamas, tuomet siurblio variklio įtampą reikia sumažinti nedaug.
3. Jei valdymo paklaida yra lygi nuliui, tuomet siurblio variklio įtampos keisti nereikia.
4. Jei valdymo paklaida yra lygi nuliui ir paklaidos kitimo greitis yra neigiamas, tuomet siurblio variklio įtampą reikia padidinti nedaug.
5. Jei valdymo paklaida yra teigiama, tuomet siurblio variklio įtampą reikia labai padidinti.

7 pav. pateikiamos skysčio lygio „fuzzy“ reguliatoriaus priklausomybės funkcijos.

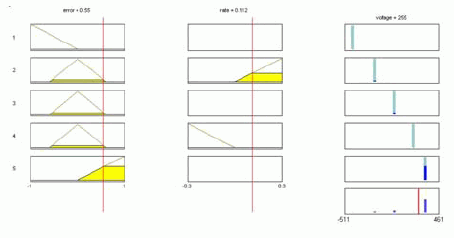
7 pav. Skysčio lygio „fuzz“y reguliatoriaus priklausomybės funkcijos (sudaryta taikant paketo MATLAB priedą „Fuzzy Logic Toolbox“)

8 pav. pateikiama lygio valdymo, panaudojant PI ir „fuzzy“ logikos reguliatorius, dinaminė charakteristika. Iš čia matyti, kad, pritaikius „fuzzy“ logikos reguliatorių, gautas kur kas geresnis rezultatas. Beveik išnyko dinaminis nuokrypis ir sumažėjo pereinamojo proceso trukmė.

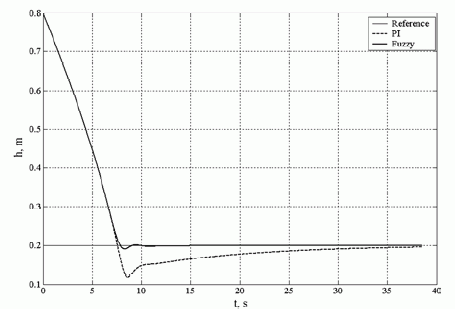
8 pav. Skysčio lygio valdymo dinaminė charakteristika, panaudojant PI (--) ir „fuzzy“ logikos (–) reguliatorius

9 pav. pateikta skysčio debito dinaminė charakteristika, kai siurblio variklis valdomas taikant tradicinį PI ir „fuzzy“ reguliatorius.

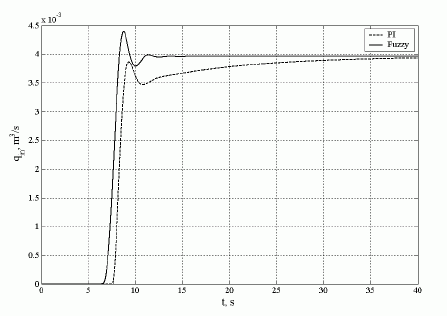
9 pav. Skysčio debito dinaminė charakteristika, siurblio varikliui valdyti naudojant PI (--) ir „fuzzy“ logikos (–) reguliatorius

Iš čia matyti, kad tradicinis PI reguliatorius įjungia siurblio variklį tik tada, kai valdymo paklaida tampa teigiama. „Fuzzy“ reguliatorius įjungia siurblį, skysčio lygiui dar nepasiekus nustatytosios vertės (esant neigiamai valdymo paklaidai). Tai leidžia labai sumažinti valdymo dinaminį nuokrypį.

Išvados

1. Sudaryti skysčio lygio valdymo sistemos matematinis ir imitacinis modeliai.
2. Išbandyti ir palyginti PI ir „fuzzy“ logikos reguliatoriai.
3. Skysčio lygiui valdyti naudojant PI reguliatorių, gaunamas didelis dinaminis nuokrypis ir labai pailgėjusi pereinamojo proceso trukmė.
4. Skysčio lygiui valdyti naudojant „fuzzy“ reguliatorių, gaunamas daug mažesnis dinaminis nuokrypis ir nedidelė pereinamojo proceso trukmė.
5. Sudaryti modeliai gali būti taikomi tolesniems tyrimams ir mokymo tikslams.

Literatūra

1. Pan H., Wong H., Kapila V., de QueirozM. S. Experimental validation of a nonlinear backstepping liquid level controller for a state coupled two tank system. // Control Engineering Practice. – Vol. 13, Issue 1, January 2005. – P.27–40.
2. Liutkevičius R., Barzdaitis V.. Netiesinio laboratorinio proceso „fuzzy“ reguliatorius. // Informacinė visuomenė ir universitetinės studijos. 2001 konferencijos pranešimų medžiaga.
3. Fuzzy Logic Toolbox for Use with MATLAB, User‘s Guide.
4. Passino K. M., Yurkovich S. Fuzzy Control. –Addison Wesley, 1998. –502 p.
5. Verbruggen H. B., Bruijn P. M.. Fuzzy control and conventional control: What is (and can be) the real contribution of Fuzzy Systems? // Fuzzy Sets and Systems. – Vol. 90 (1997). –P. 151–160.
6. Ljung L., Glad T.. Modeling of dynamic systems.– Englewood Cliffs: Prentice Hall, 1994. –361 p.

G. Valiulis. Skysčio lygio valdymas taikant fuzzy logiką // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2005.– Nr.8(64). – P. 65–68.