Įvadas
Medicininių vaizdų analizė yra svarbus ligos diagnozavimo, kurį atlieka rentgenologai, interpretuodami vaizduose esančią informaciją, etapas. Galutinei diagnozei turi įtakos objektyvios ir subjektyvios priežastys. Kompiuterinėje tomografijoje gaunami mažo kontrasto pilkieji vaizdai, kurių net nedidelis patamsėjimas gali reikšti sunkią ligą [1]. Žmogaus galimybės aptikti objektus pilkuosiuose vaizduose yra ribotos, nes jis sugeba atskirti tik nedidelį pilkumo lygių skaičių. Diagnozės patikimumą bei spartą galima padidinti, naudojant kompiuterinę vaizdų apdorojimo įrangą, gebančią analizuoti įvairaus dydžio ir daug pilkumo lygių turinčius vaizdus.
Šiame straipsnyje nagrinėjamos galimybės taikyti vilnelių (angl. wavelets) transformaciją kompiuterinių tomogramų (KT) vaizdams analizuoti. Vilnelių transformacijos metodas lyginamas su kitais išeminio insulto sričiai aptikti taikomais metodais, analizuojamas vilnelių spektro dedamųjų sąryšis su insulto sritimi bei rekomenduojami galimi būdai insulto sričiai aptikti.
Vilnelių transformacijos metodo privalumai
Išeminio insulto sričiai aptikti taikomi laikiniai ir dažniniai metodai.
Dauguma žinomų metodų yra laikiniai. Jais apdorojant bei analizuojant vaizdus, naudojami pradinio bei tarpinių vaizdų taškai. Galima teigti, kad rentgenologai, vizualiai analizuodami tomogramas, taip pat taiko laikinius metodus, nes analizės metu jie netransformuotose tomogramose ieško insultą nurodančio patamsėjimo, įvertina jo formą, padėtį smegenų pusrutuliuose ir dydį. Insulto nustatymui automatizuoti yra išmėginti histogramos, momentų, Markovo laukų, neuronų tinklų, smegenų pusrutulių palyginimo bei kiti metodai. Dauguma jų remiasi insulto srities patamsėjimo ar kitokiais ligos požymiais originalioje tomogramoje [2]. Laikiniai metodai yra labai įvairūs. Iki šiol neturime universalaus algoritmo, kuris kompiuterinėse tomogramose galėtų tiksliai pažymėti insultą ir apskaičiuoti jo tūrį. Tai yra susiję tiek su paties insulto savybėmis, tiek su šių savybių matematiniu aprašymu.
Galvos smegenų KT vaizdams apdoroti ir analizuoti galima taikyti ir dažninius metodus. Nemaža dažninių metodų yra pagrįsti Fourier‘o transformacija, kurios metu apskaičiuojamas dvimatis tomogramos spektras. Apdorojant spektrą galima paryškinti arba panaikinti periodines vaizdų dedamąsias, taip pat sumažinti triukšmą. Galvos smegenų KT vaizdų spektruose nėra griežtai periodinių struktūrų. Išeminis insultas spektre yra susijęs su žemojo dažnio dedamosiomis, kurias išskiriant žemojo dažnio filtru (ŽDF) galima pašalinti smulkiuosius KT vaizdo objektus, nesusijusius su insulto sritimi. Taikant ŽDF, ne visais atvejais galima atskirti insulto sritį nuo įprastinių KT vaizdo objektų, turinčių panašų kaip insultas skaistį ir dydį. Insulto sričiai tiksliai išskirti būtina naudoti sudėtingus filtrus, įvertinančius dažninius amplitudės ir dažninius fazės išeminio insulto požymius.
Vaizdams apdoroti taikomi ir laikiniai dažniniai metodai. Vaizdo spektrui gauti galima taikyti vilnelių transformaciją, kuri leidžia atlikti nestacionarių signalų spektrinę analizę ir įvertinti spektro pokyčius laikui bėgant.
Vaizdus apdorojant vilnelių transformacija yra naudinga signalų glaudinimo [3], dekompozicijos [4, 5], taip pat rašto atpažinimo [6], kontūrų nustatymo [7], triukšmo mažinimo [8] ir pan. uždaviniuose. Šie taikymai yra aktualūs ir KT vaizdų apdorojimui, nes juos galima apibūdinti kaip nestacionarius dvimačius signalus, paveiktus triukšmo. Viena iš jų nestacionarumo priežasčių yra išeminis insultas. Vilnelių transformacija šiuo atveju naudinga kaip dekompozicijos operacija, išskaidanti vaizdą į dedamąsias, kurių analizė yra paprastesnė nei viso vaizdo. Kompiuterinių tomogramų vaizdų eilučių analizė Vienmačio tolydžiojo signalo s(t) vilnelių transformacija užrašoma lygtimi [9]
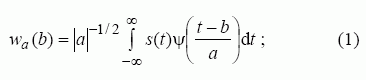
čia wa(b) yra vilnelių spektro funkcija, ψ(•) – vilnelės funkcija, a – mastelio koeficientas, b – poslinkis. Diskrečiųjų signalų, kurių trukmė yra baigtinė ir kartotinė dviem, transformacijai (1) formulę galima užrašyti atitinkama suma:
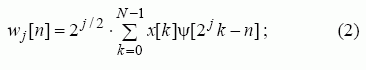
čia wj[n] – diskrečioji vilnelių spektro funkcija; x[k] – diskrečiojo signalo vertė; ψ[•] – diskrečioji vilnelės funkcija; j = 0, 1,…, R – 1 – mastelio rodiklis, apibūdinantis 74 vilnelės trukmę; n = 0, 1,…, 2j – 1 – vilnelės poslinkis laiko ašyje; k = 0, 1,…, N – 1 – signalo imties numeris diskrečiojo laiko ašyje; N = 2R – signalo imčių skaičius; R – sveikasis teigiamas skaičius. (1) ir (2) formulėse vilnelės mastelio rodiklis ir maksimalus poslinkis tarpusavyje susiję: kuo mastelio rodiklis didesnis, tuo vilnelė trumpesnė ir galimas jos poslinkis didesnis. Vilnelių funkcijos ψ(•) yra osciliacinio pobūdžio, turi nulinį vidurkį, baigtinę normą ir sudaro ortogonaliųjų funkcijų rinkinį. Šiuos reikalavimus atitinka daug įvairių vilnelių, pavyzdžiui, Morlet, FHAT, MHAT („sombrero“), Daubechies [9] ir kt. Vilnelės gali būti ir kompleksinės. Vilnelės parinkimas priklauso nuo analizuojamo signalo pobūdžio ir uždavinio formulavimo.
Kompiuterinės tomogramos eilutės yra vienmačiai diskretieji baigtinės trukmės signalai. KT transformuoti sparčiaisiais skaitmeniniais algoritmais tikslinga pasirinkti nesudėtingos formos vilnelę, pavyzdžiui, Haaro vilnelę.
Trumpiausios diskrečiosios Haaro vilnelės, kai mastelio rodiklis j = R – 1, ir vilnelės, kai j = R – 2, yra pavaizduotos 1 pav. Paveiksle brūkšninėmis linijomis pavaizduotos analogiškos tolydžiojo laiko t vilnelės ψj,n(t) = ψ(2jt – n), atsižvelgiant į tai, kad mastelio koeficientas a = 2–j, o vilnelės poslinkis b = a•n. Matyti, kad, mažinant mastelio rodiklį j, vilnelė ilgėja. Ši vilnelės savybė leidžia atspindėti signalo x[k] kitimo spartą. Parametras n nusako vilnelės padėtį laiko ašyje, todėl vilnelių spektre matyti signalo spektrinė sudėtis dominančiu laiko momentu. Vilnelės poslinkio žingsnis laiko ašyje didėja, smulkėjant masteliui (mažėjant j) taip, kad vilnelių funkcijos būtų ortogonalios.
Tuo galima įsitikinti sudauginus ir susumavus laiko ašyje dvi bet kurias vilnelių funkcijas, pavaizduotas 1 pav.
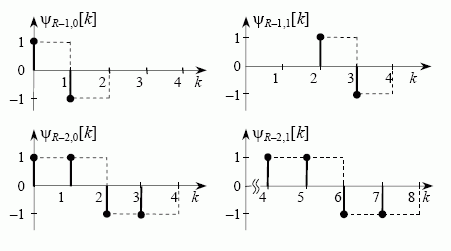
1 pav. Diskrečiosios Haaro vilnelės, esant skirtingiems mastelio rodikliams j ir poslinkiams n laiko ašyje
Apskritai Haaro vilnelių funkcijos užrašomos tokia apibendrintąja lygtimi:
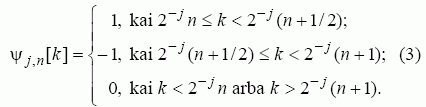
reikia R = log2N skirtingo mastelio vilnelių, kurių kiekvieną reikia apskaičiuoti pagal (3) formulę ir paslinkti laiko ašyje 2j kartų. Vilnelių spektro skaičiavimą galima nutraukti bet kuriuo j = J masteliu. Tuomet išskaidytąją signalo dalį apibūdina jau apskaičiuoti vilnelių koeficientai, o likusioji, neišskaidytoji, signalo dalis užrašoma panaudojant mastelio funkcijas. Be to, naudojant mastelio funkciją galima supaprastinti vilnelių spektro skaičiavimą, nes (2) formulę galima perrašyti rekursiniu pavidalu ir skaičiavimuose naudoti tik po vieną vilnelės ir mastelio funkciją. Diskrečiosios mastelio funkcijos, skirtos naudoti kartu su diskrečiosiomis Haaro vilnelėmis, apibūdinamos tokia išraiška:
Mastelio funkcijos φj,n[k], kurių mastelio rodiklis j = R – 1 ir j = R – 2, yra pavaizduotos 2 pav. Šiame paveiksle brūkšninėmis linijomis pateiktos diskrečiąsias mastelio funkcijas atitinkančios tolydžiojo laiko t funkcijos φj,n(t) = φ(2jt – n). Palyginę vilnelių ir mastelio funkcijas, matome, kad jos analogiškos vilnelių funkcijoms, tik mastelio funkcijos visuomet yra teigiamos. Poslinkio n požiūriu mastelio funkcijos, esant fiksuotam mastelio rodikliui j, visuomet sudaro ortogonaliųjų funkcijų rinkinį.
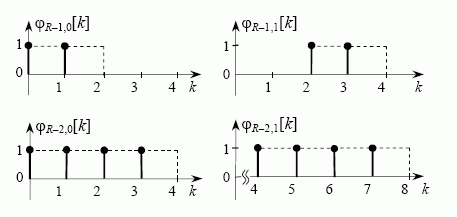
2 pav. Diskrečiosios mastelio funkcijos, esant skirtingiems mastelio rodikliams j ir poslinkiams n laiko ašyje
Vilnelių ir mastelio funkcijų normos tarpusavyje vienodos ir lygios: ||ψj,n|| = ||φj,n|| = 2–j/2.
Nutraukus signalo x[k] vilnelių transformaciją masteliu j = J, neišskaidytoji jo dalis apibūdinama aproksimacijos koeficientais cJ[n], apskaičiuojamais taip:
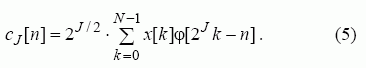
Pagal (5) formulę apskaičiuoti aproksimacijos koeficientai cJ[n] atitinka signalą x[k], gaunamą ŽDF, turinčio N·2J–R–1 pločio stačiakampę dažninę amplitudės charakteristiką, išėjime. Vilnelių koeficientai, apskaičiuoti pagal (2) lygtį, atitinka aukštojo dažnio filtro (ADF) išėjimo signalą. Šio filtro ribinis dažnis lygus ŽDF ribiniam dažniui. Taigi, esant fiksuotam mastelio rodikliui j = J, signalą x[k] visiškai apibūdina jo vilnelių ir aproksimacijos koeficientai.
Turint aproksimacijos koeficientus cJ[n] ir norint išanalizuoti mastelio j = J – 1 signalą, nebūtina taikyti (2) formulę, pakanka tarti, kad analizuojamąjį signalą sudaro aproksimacijos koeficientų seka, ir jos transformacijai taikyti trumpiausiąją vilnelę. Tai leidžia vilnelių transformaciją užrašyti rekursiniu pavidalu, kai kiekvienoje rekursijoje skaičiuojami vilnelių ir aproksimacijos koeficientai, laikant, kad analizuojamasis signalas yra ankstesnės rekursijos aproksimacijos koeficientų seka. Atidžiau išnagrinėjus (2) – (5) išraiškas, matyti, kad smulkiausiojo mastelio Haaro vilnelių koeficientai skaičiuojami nuosekliai imant signalo x[k] imčių poras ir nustatant jų skirtumą. Aproksimacijos koeficientai apskaičiuojami sudedant tas pačias signalo imčių poras. Iš to išplaukia rekursinės vilnelių transformacijos formulės:
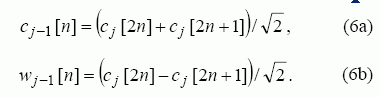
Vilnelių transformacijos metu pirmiausia apskaičiuojami smulkiausiojo mastelio aproksimacijos cR –1[n] ir vilnelių wR –1[n] koeficientai. Jam apskaičiuoti naudojamos analizuojamojo signalo x[k] imtys. Taigi skaičiuojant koeficientus, (6a) ir (6b) išraiškose reikia imti j = R, cR[2n] = x[k], kai k = 0, 2,..., N – 2, ir cR[2n + 1] = x[k], kai k = 1, 3,..., N – 1. Toliau, diskretiškai mažinant mastelio rodiklį j, apskaičiuojami kiti vilnelių bei aproksimacijos koeficientai. Vėliau jie taikomi kitose rekursijose. Rekursijos baigiamos, kai mastelio rodiklis j = 0. Šios rekursijos metu apskaičiuojami du koeficientai – c0[0] ir w0[0]. Koeficientas c0[0] vilnelių spektre nepateikiamas, jo vertė yra proporcinga signalo vidurkiui.
KT vaizdo vienos eilutės x[k] vilnelių transformacijai buvo panaudoti vaizdai su insulto sritimi ir be jos. Analizuotas KT vaizdas su insulto sritimi yra parodytas 3 pav., a, o greta, 3 pav., b, pateiktas analogiškas vaizdas be insulto srities. Tai modelis, gautas panaikinus iš 3 pav., a, insulto sritį. Be to, prieš vilnelių transformaciją iš analizuotų KT buvo pašalinti visi vaizdo objektai, nepriklausantys smegenų sričiai, ir vaizdo fonas buvo užpildytas taškais, kurių skaistis atitinka smegenų srities skaisčio vidurkį. Toks vaizdų paruošimas leido tiksliau įvertinti vilnelių koeficientų pokyčius, susijusius su insulto sritimi. Netaikant pradinio paruošimo, didžiausi vilnelių koeficientai buvo gauti ties kaulo ir smegenų bei odos ir fono vaizdo sričių sąlyčiu. Tuo tarpu insulto srityje koeficientų vertės visuomet yra nedidelės.
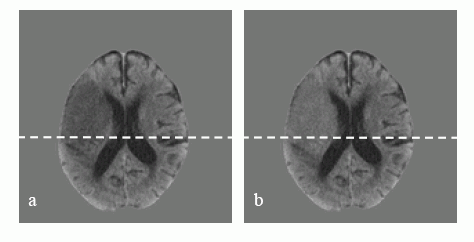
3 pav. KT vaizdas su insulto sritimi (a) ir be jos (b)
KT vaizdų su insulto sritimi ir be jos pavienių eilučių skaisčio grafikai parodyti 4 pav., a. Šios eilutės yra pažymėtos 3 pav. balta brūkšnine linija. Eilučių skaisčio grafikai vaizduose su insulto sritimi ir be jos skiriasi tik ties insulto sritimi. Insulto sritis nagrinėjamoje eilutėje, kai k є (100, 200), pastebima kaip tolydi ir lokali skaisčio verčių sumažėjimo vieta.
Kiekvienoje KT vaizdo eilutėje yra 512 (t. y. 29) taškų. Atliekant pasirinktos eilutės vilnelių transformaciją, (6a) ir (6b) formules reikia taikyti 9 kartus. Eilutėje visų taškų skaisčio vertės yra teigiamos ir kinta nuo 60 iki 140.
Vilnelių koeficientai wj[n] buvo gauti teigiami bei neigiami ir kito didesniame verčių diapazone. Vaizduojant vilnelių spektrą, vertikaliojoje ašyje patogu atidėti normuotąsias koeficientų vertes. Horizontaliosios plokštumos vienoje iš ašių yra atidedamas mastelio rodiklis j, o kitoje – poslinkis n. Taip vizualizuotas vilnelių spektras parodytas 4 pav., b.
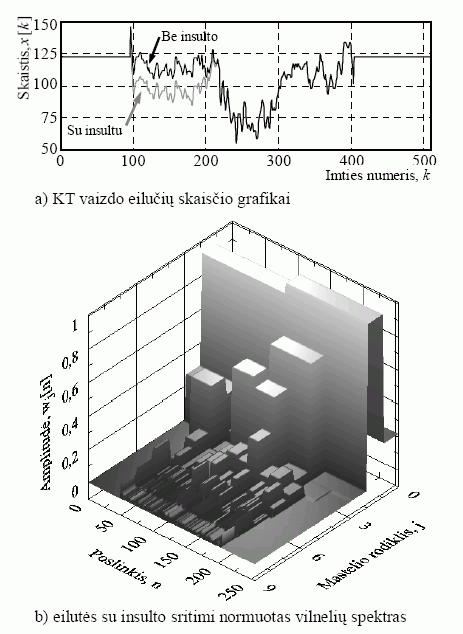
4 pav. KT vaizdo eilutės vilnelių transformacijos rezultatai
Iš 4 pav., b, matyti, kad intensyviausios vilnelių spektro dedamosios yra žemųjų dažnių srityje, nes jos yra ties mažiausiais mastelio rodikliais. Didėjant rodikliui j, vilnelių koeficientų absoliutinės vertės staigiai mažėja, tačiau mažėjimo pobūdis priklauso nuo poslinkio n, t. y. nuo signalo analizės vietos. Kai mastelio rodiklis j yra sąlygiškai didelis, vilnelių koeficientų vertės yra mažos ir susitelkusios poslinkio n intervale (50, 200). Kai j yra mažas, spektre energija pasiskirsto platesniame intervale. Kai j = 0, gaunama vienintelė vilnelė, apimanti visą KT vaizdo eilutę. Šios vilnelės koeficientas apibūdina žemiausiojo dažnio dedamosios amplitudę.
Norint išsiaiškinti, kaip KT vaizdo eilutės vilnelių spektrą pakeičia insulto sritis, buvo palyginti eilutės su insulto sritimi ir be jos vilnelių spektrai. 5 pav. parodyta, kokie koeficientai ir kiek pasikeitė KT vaizdo eilutėje atsiradus insulto sričiai. Šiame paveiksle matyti, kad didžiausi skirtumai atsiranda žemųjų dažnių srityje. Esant mastelio koeficientams j = 1, 2, 3, jie akivaizdžiai pastebimi poslinkio n intervale (0, 128). Žemiausiojo dažnio dedamoji padidėja nedaug, nes insulto sritis yra palyginti didelė ir jos skaistis nedaug mažesnis už sveikų smegenų srities skaistį. Kai j ≥ 1, dešiniojoje spektro dalyje, ties n = 128 ÷ 256, pokyčių nėra. Tai rodo, kad insulto sritis KT vaizdo eilutės spektre yra lokalizuota. Didžiausi spektro pokyčiai matomi kairiojoje jo pusėje. Spektro srityse, kai j = 2, n = 0 ÷ 64 ir j = 3, n = 32 ÷ 64, koeficientų absoliutinės vertės išauga iki 4 kartų. Greta nurodytų spektro dedamųjų, kai j = 2, n = 64 ÷ 128 ir j = 3, n = 64 ÷ 96, koeficientai sumažėja iki 10 kartų. Tai rodo, kad insulto sritis ryškiai pakeičia kai kurių žemojo dažnio dedamųjų amplitudes: jas sumažina arba padidina. Koeficientai padidėja, kai insulto sritis išsiskiria KT vaizdo fone, o sumažėja – kai greta insulto srities yra kitų sričių, turinčių panašų ar mažesnį už insulto srities skaistį. Nagrinėjamoje KT eilutėje iš kairiosios pusės yra fono sritis, o iš dešiniosios – mažo skaisčio sritis. Kai j = 4, tarp koeficientų dar pastebimi pokyčiai, tačiau didžioji jų dalis lieka nepakitusi, be to, koeficientų absoliučiosios vertės yra mažos ir jų pokyčiai nedideli. Kai mastelio rodiklis viršija 4, spektruose pokyčių beveik nebelieka. Taigi iš spektrų palyginimo išplaukia, kad insulto srities reikia ieškoti vilnelių spektro žemųjų dažnių srityje, analizuojant lokaliai išsidėsčiusių koeficientų grupes.
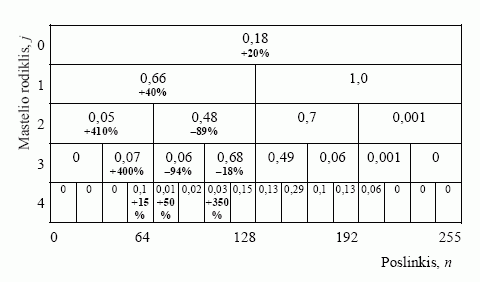
5 pav. Modeliuoto ir originalaus vaizdo eilučių vilnelių spektrų palyginimas
Kompiuterinių tomogramų vaizdų vilnelių transformacija
Vaizdai yra dvimačiai signalai, kurie apibūdinami skaisčio pasiskirstymo matricomis. Jų vilnelių spektrui apskaičiuoti naudojamos formulės, skirtos vienmačiams signalams. Vienas iš paprastesnių vilnelių spektro nustatymo būdų yra analogiškas dvimačio Fourier‘o spektro skaičiavimui, naudojant eilučių stulpelių algoritmą. Pagal šį algoritmą (6a) ir (6b) formules reikia taikyti iš pradžių eilutėms, o po to stulpeliams. Galutinis skaičiavimo rezultatas nesikeičia, jeigu pirma apdorojami stulpeliai, o vėliau – eilutės. Skirtingai nei vienmačiu atveju, dvimačio signalo analizės metu, esant fiksuotam mastelio rodikliui, gaunami trijų tipų vilnelių koeficientai.
Atliekant vaizdų analizę, aproksimacijos ir vilnelių koeficientus įprasta žymėti s (angl. sum) ir d (angl. difference). Taigi pritaikius rekursines formules tik eilutėms, gaunamos koeficientų matricos s(j) ir d(j), kurios yra eilučių kryptimi dvigubai mažesnės už pradinio vaizdo matricą. Toliau analogiškos rekursinės formulės taikomos gautųjų s(j) ir d(j) matricų stulpeliams. Pritaikius s(j) matricos stulpeliams sumavimo operaciją, gaunama aproksimacijos koeficientų matrica ss(j), o jei taikoma atimties operacija, gaunama matrica sd(j). Tuos pačius veiksmus pritaikius d(j) matricai, gaunamos ds(j) ir dd(j) matricos. Aptarti veiksmai turi būti kartojami kiekvienu masteliu j, laikant, kad analizuojamas vaizdas yra ankstesniojo rekursinio žingsnio metu gauta matrica ss(j). Skaičiuojant vilnelių koeficientus, matricos s(j) ir d(j) yra tarpiniai rezultatai, kuriems laikinai saugoti reikia atskirų atminties masyvų. Jų galima išvengti, jeigu naudojamos (7a) – (7d) formulės, leidžiančios apskaičiuoti vilnelių ir aproksimacijos koeficientus pagal vaizdo taškų ketvertus. Skaičiavimo pradžioje reikia tarti, kad pradinis vaizdas atitinka koeficientų matricą ss(R) ir j = R.
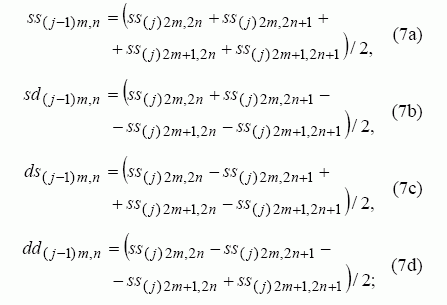
čia m = 0, 1,..., 2j–1–1 – vilnelės poslinkis eilutėje, atitinkantis aproksimacijos koeficientų imties numerį; n = 0, 1,..., 2j–1–1 – vilnelės poslinkis stulpelyje, atitinkantis aproksimacijos koeficientų imties numerį. Veiksmai, kuriuos aprašo (7a) – (7d) formulės, dažnių srityje atitinka vaizdo imčių porų eilutėse ir stulpeliuose filtravimą žemojo ir aukštojo dažnio filtrais. Atsižvelgiant į tai, KT vaizdo vilnelių transformaciją galima pavaizduoti 6 pav. schema.
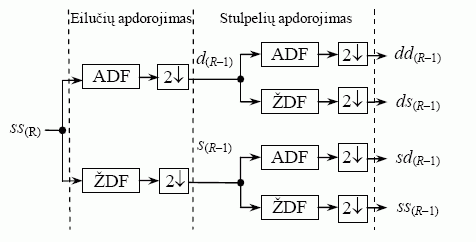
6 pav. KT vaizdo vilnelių transformacijos pirmosios rekursijos schema
Standartinis KT vaizdas yra 512×512 (29×29) taškų dydžio. KT vaizdo transformacijos vilnelėmis metu jis pirmiausia prilyginamas matricai ss(9). Po to iš (7a) – (7d) formulių gaunamos trys vilnelių koeficientų matricos: sd(8), ds(8), dd(8), taip pat aproksimacijos koeficientų matrica ss(8).
Visos šios matricos yra 256×256 dydžio. Matrica ss(8) yra KT vaizdas, kurio eilutės ir stulpeliai yra nufiltruoti ŽDF. Iš šio vaizdo pašalintos aukštųjų dažnių spektro dedamosios. Kitu vilnelių transformacijos žingsniu iš ss(8) galima apskaičiuoti sd(7), ds(7), dd(7) ir ss(7) matricas, kurių dydis yra 128×128. Rekursinį vilnelių koeficientų skaičiavimą galima tęsti, kol matricos sumažėja iki vieno elemento (j = 0). Nuosekliai transformavus KT vaizdą nuo j = 8 iki j = 0, gaunamas visas vaizdo Haaro vilnelių spektras.
Kompiuterinių tomogramų vaizdų vilnelių spektro analizė
KT vaizdo vilnelių spektras masteliais j = 3 ÷ 8 yra pavaizduotas 7 pav. Vaizdo vilnelių spektro matricas yra įprasta išdėstyti pradinio vaizdo dydžio kvadrate, kurio įstrižainėje yra dd koeficientų matricos, o matricos sd ir ds atitinkamai yra išdėstytos vertikaliai ir horizontaliai. Paveikslo apačioje matyti analizės rezultatai, gauti smulkiausiu masteliu (j didžiausias). Mastelio rodiklis j mažėja, kylant į viršų ir artėjant prie kairiojo viršutinio paveikslo kampo. Matyti, kad mastelis kaskart kinta dvigubai, todėl analizės matricos mažėja labai sparčiai. Matricų vaizdai, kai j ≤ 5, paveiksle yra padidinti 8 kartus. Stambiausių mastelių, kai j ≤ 2, vilnelių koeficientų matricos nepavaizduotos.


7 pav. Kompiuterinės tomogramos Haaro vilnelių spektras
7 pav. matyti, kad smulkiausiojo mastelio vilnelių koeficientai atspindi mažiausius vaizdo objektus. Juose galima įžvelgti tik smulkiausias vaizdo detales bei triukšmo pavidalo foną. Reikia pasakyti, kad koeficientai sd yra susiję su tomis vaizdo detalėmis, kurios yra pailgos ir orientuotos vertikaliai. Koeficientai ds apibūdina horizontaliai išsidėsčiusius objektus, o koeficientai dd – objektus, kurie išsidėstę vaizdo įstrižainių kryptimis. Pavyzdžiui, matricoje sd(8) puikiai matyti vertikali didžiųjų smegenų pusrutulių pertvara, matricoje ds(8) matyti kai kurie horizontalūs smegenų vingiai. Stambėjant masteliui, vilnelių koeficientai pradeda apibūdinti vis stambesnių KT vaizdo objektų kontūrus. Tarkime, matricoje sd(5) išsiskiria X raidės pavidalo tamsaus smegenų objekto kontūrai.
Kontūrą atitinka teigiami vilnelių koeficientai, kai analizuojant pereinama nuo fono srities į tamsaus objekto sritį, ir neigiami koeficientai, kai pereinama iš tamsaus objekto srities į šviesesnę fono sritį. Kuo objektas labiau išsiskiria bendrame fone, tuo absoliutinės vilnelių koeficientų vertės yra didesnės.
Analizuojant vilnelių koeficientus insulto srityje, pastebėta, kad jos kontūrą atspindintys koeficientai yra nedideli ir jų absoliučiosios vertės artimos sveikų smegenų sričių koeficientams. Toks rezultatas gaunamas, nes insulto srities skaistis nedaug skiriasi nuo vaizdo fono skaisčio.
Be to, insulto sritis yra vienalytė ir jos skaistis sumažėjęs tolydžiai. Tai reiškia, kad insulto srityje, neskaitant jos kontūro, vilnelių koeficientų vertės nesiskiria nuo fono srities koeficientų verčių. Remiantis šiais teiginiais galima siūlyti dvi insulto automatinio nustatymo strategijas: pirmoji gali remtis kontūro koeficientų nustatymu, antroji – srities koeficientų nustatymu. Pirmuoju atveju reikia ieškoti vienodų insulto srities kontūrui būdingos absoliučiosios vertės vilnelių koeficientų, nes insulto sritis yra tolygiai patamsėjusi ir skaisčio pokyčiai tarp fono ir insulto srities arba atvirkščia kryptimi turėtų duoti panašaus dydžio vilnelių koeficientus visomis paieškos kryptimis. Antras būdas yra grindžiamas insulto srities vienalytiškumu, todėl ją atitinkantys vilnelių koeficientai yra artimi nuliui nepriklausomai nuo analizės krypties. Abiem atvejais analizę tikslinga pradėti nuo žemiausiųjų dažnių (stambiausių mastelių) koeficientų, nes insulto sritis paprastai užima didelę vaizdo dalį ir ją gana gerai atspindi j = 1 ÷ 3 mastelio rodiklio vilnelių koeficientų matricos.
Išvados
- Pagrindinis vilnelių transformacijos taikymo pranašumas, palyginti su laikiniais bei dažniniais metodais, yra galimybė analizuoti nestacionarių signalų spektro pokyčius laikui bėgant.
- Galvos smegenų kompiuterinės tomogramos vaizde atsiradus insulto sričiai, atskirų jos eilučių Haaro vilnelių spektras labiausiai pasikeičia žemųjų dažnių srityje. Insulto srities atsiradimas net tuomet, kai ji silpnai išsiskiria bendrame fone, gali pakeisti kai kurių vilnelių koeficientų amplitudes 10 kartų.
- Kompiuterinių tomogramų vaizdų Haaro vilnelių spektrus kiekvienu masteliu sudaro trijų tipų dedamosios, kurios apibūdina vaizdo objektų kontūrus horizontalia, vertikalia ir įstriža kryptimi. Tinkamai nustačius, išskyrus ir sugrupavus kontūrų elementus, galima tiksliai nustatyti insulto srities kontūrą kompiuterinėje tomogramoje.
- Išeminio insulto srities kontūrui rasti kompiuterinės tomogramos vaizde reikia Haaro vilnelių spektre nustatyti žemųjų dažnių koeficientus, išsidėsčiusius uždaru kontūru ir turinčius tik insulto kontūro sričiai būdingas vertes. Kitas būdas visai insulto sričiai rasti yra pagrįstas artimų nuliui vilnelių koeficientų išskyrimu.
- Siūlomais būdais KT vaizde bus aptinkama tik vienalytė tolygiai sumažėjusio skaisčio insulto sritis.
Padėka
Straipsnis parengtas vykdant EUREKA projektą E!2981, kurį finansuoja Lietuvos valstybinis mokslo ir studijų fondas (sutarties Nr. V-27).
Literatūra
- König M., Klotz E., Heuser L. Diagnosis of cerebral infarction using perfusion CT: state of the art // Electro Medica. A periodical for medicine and medical systems, 2000. – Vol. 68, Nr. 2. – P. 9–12.
- Ušinskas A., Kirvaitis R. Žmogaus galvos smegenų ischeminio insulto automatinės analizės metodų apžvalga // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2003. – Nr.7(49). – P. 52–59.
- Pūnienė J., Navickas R., Pūnys V., Jurkevičius R. Statistinis tyrimas medicininių vaizdų suspaudimui „bangelių“ transformacijos metodu įvertinti // Medicina. – Kauno medicinos universitetas, 2002. – Nr. 38(2). – P. 210– 213.
- Unser M., Aldroubi A. A review of wavelets in biomedical applications // Proceedings of the IEEE. – 1996. – Vol. 84, No. 4. – P. 626–638.
- Дремин М. И., Иванов О. В., Нечитайло В. А. Вэйвлеты и их использование // Обзоры актуальных проблем. – Москва: Физический институт им. П. Н. Лебедева, 2001. – Т. 171, № 5. – С. 465–501.
- Cristobal G., Fischer S., Forero-Vargas M., Redond R. Texture segmentation and analysis using local spectral methods. – Instituto de Optica Imaging and Vision Department, 2003. – 4 p.
- Baušys R., Leonavičius G. Wavelet-based edge detection // Informacinės technologijos‘2004. Konferencijos pranešimų medžiaga. – Kauno technologijos universitetas, 2004. – P. 13–17.
- Mertins A. Signal Analysis: Wavelets, Filter Banks, Time- Frequency Transforms and Applications. – John Wiley & Sons Ltd., 1999. – P. 261–264.
- Баскаков С.И. Радиотехнические цепи и сигналы. – Москва: Высшая школа, 2003. – С. 65–68.
V. Mikelaitis, R. Martavičius, E. Žitkevičius. Vilnelių transformacijos taikymas žmogaus galvos smegenų kompiuterinių tomogramų su insulto sritimi analizei // Elektronika ir elektrotechnika. – Kaunas: Technologija, 2005. – Nr. 8(64). – P. 73–78.


 Medicininių vaizdų analizė yra svarbus ligos diagnozavimo, kurį atlieka rentgenologai, interpretuodami vaizduose esančią informaciją, etapas. Galutinei diagnozei turi įtakos objektyvios ir subjektyvios priežastys. Kompiuterinėje tomografijoje gaunami mažo kontrasto pilkieji vaizdai, kurių net nedidelis patamsėjimas gali reikšti sunkią ligą.
Medicininių vaizdų analizė yra svarbus ligos diagnozavimo, kurį atlieka rentgenologai, interpretuodami vaizduose esančią informaciją, etapas. Galutinei diagnozei turi įtakos objektyvios ir subjektyvios priežastys. Kompiuterinėje tomografijoje gaunami mažo kontrasto pilkieji vaizdai, kurių net nedidelis patamsėjimas gali reikšti sunkią ligą.