Įvadas
Savo gyvenime kiekvienas iš mūsų susiduria su įvairiais signalais, tačiau ne visada tai yra taip akivaizdu, kaip atrodo. Signalas yra bet koks fizikinis informacijos nešiklis, be jo neįmanoma informacijos perduoti, saugoti, apdoroti, atkurti. Net kai du žmonės tarpusavyje kalbasi, tai yra signalų generavimas, atkūrimas, perdavimas, konvertavimas, filtravimas, apdorojimas. Kaip žinome, žmogaus smegenys yra sudarytos iš neuroninių tinklų, o atskiri neuronai elektrinius signalus siunčia, priima, apdoroja, filtruoja. Kai atminties ląstelės perduoda neuronams elektrinius impulsus, tai yra signalų generavimas. Kai kalbame, mūsų balso stygos elektrinius signalus konvertuoja į oro sutankėjimus ir praretėjimus. Kito žmogaus ausis šiuos „slėgio signalus“ vėl paverčia elektriniais signalais. Šio žmogaus neuroniniai tinklai analizuoja informaciją: filtruoja, apdoroja, o prireikus ir išsaugo. Visame šitame cikle svarbią vietą užima filtravimas – tai yra labai svarbus procesas, kuris padeda atrinkti reikalingą informaciją nuo bereikalingos bei padeda atstatyti sugadintus ar iškraipytus signalus.
Šiame darbe aptarsime skaitmeninius filtrus. Bendriausiu atveju, filtras – priemonė signalui filtruoti. Skaitmeniniai filtrai nuo analoginių skiriasi tuo, kad filtravimas atliekamas kompiuteryje ar signalų procesoriuje, be to, skaitmeniniai filtrai leidžia pasiekti daug geresnių rezultatų, nei analoginiai.
„Sinc“ filtras
Vienas iš skaitmeninių filtrų pavyzdžių – „sinc“ filtrai su langu. Dažniausiai jie naudojami vienų dažnių atskyrimui nuo kitų. „Sinc“ filtrai yra labai stabilūs, o jų charakteristikas galima tobulinti iki begalybės. Šios išskirtinės savybės dažnio srityje gaunamos prarandant kokybę laiko srityje, įskaitant atsirandančius bangavimus (angl. ripple) bei lygio viršijimus atsake. Naudojant standartinę konvoliuciją, „sinc“ filtrus su langu lengva suprogramuoti, tačiau jie lėtai vykdomi.
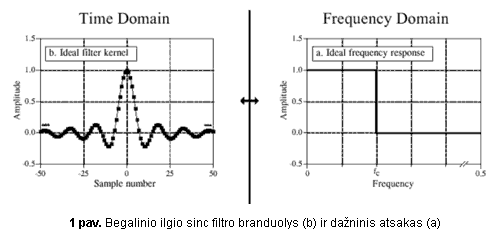
Kaip matyti iš 1 pav., idealaus žemų dažnio filtro branduolys gali idealiai nufiltruoti aukštus dažnius: visi dažniai žemiau fc yra praleidžiami, o visi, esantys virš fc – blokuojami. Praleidžiamų dažnių juosta yra idealiai lygi, slopinimas užtvarinėje srityje yra begalinis, o perėjimas tarp šių juostų yra be galo mažas.
Apibrėšime idealaus žemų dažnių filtro branduolio matematinę išraišką, ji vadinama sinc fukcija (iš čia ir filtro pavadinimas):
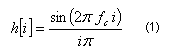
„Sinc“ filtro panaudojimo problemos. Konvoliuojant įeinantį signalą su šiuo filtro branduoliu gausime idealų žemų dažnių filtrą. Problema yra tame, kad „sinc“ funkcija yra begalinė tiek į teigiamų, tiek ir į neigiamų skaičių pusę ir funkcijos vertė niekada visiškai nesumažėja iki nulio. Matematikos mokslui šis begalinis ilgis nėra jokia problema, tačiau kompiuteris negali nei priimti, nei apdoroti begalinio taškų skaičiaus funkcijos.
Šiai problemai spręsti naudojamas toks metodas:
- a) filtro branduolį reikia sutrumpinti iki M+1 taško (M – pasirinkta konstanta – lyginis natūralusis skaičius),
- b) visus taškus, esančius toliau M+1 taško užpildome nuliais,
- c) filtro branduolį perstumiame į dešinę, kad jis užimtų taškus nuo 0 iki M.
Taigi praktiškai mes apsiribojame tam tikru baigtiniu sinc funkcijos taškų skaičiumi. Tokio filtro branduolys ir jo atsakas pateiktas 2 pav. Kaip matyti, neidealus filtras duoda neidealų atsaką: labai ryškūs pabangavimai praleidimo srityje ir gana prastas slopinimas užtvarinėje srityje. Šios problemos atsiranda dėl filtro branduolio taškų skaičiaus baigtinumo. Kaip bebūtų gaila, didinant filtro branduolio ilgį, atsiradusių problemų išspręsti neina.
Laimei, egzistuoja gana paprastas būdas, leidžiantis nors ir ne visiškai, tačiau bent dalinai išspręsti problemą. Tam reikia panaudoti taip vadinamą langą (lango pavyzdys – 2 pav., e). Sudauginus baigtinio taškų skaičiaus „sinc“ filtro branduolį su tokiu langu su gausime „sinc“ filtrą su langu (3 pav., f). Lango panaudojimo esmė ir tikslas yra tame, kad baigtinio taškų skaičiaus „sinc“ filtro dažninį atsaką gadina ne tiek pats taškų skaičiaus baigtinumas, kiek netolydžiai sumažėjantys filtro branduolio kraštai. Todėl užglotninus filtro branduolio kraštus, žymiai pageriname filtro dažninį atsaką: nebelieka bangavimų, o slopinimas užtvarinėje srityje padidėja. Tačiau pastebėtina ir tai, kad praplatėjo perėjimas tarp praleidimo ir užtvarinės srities.
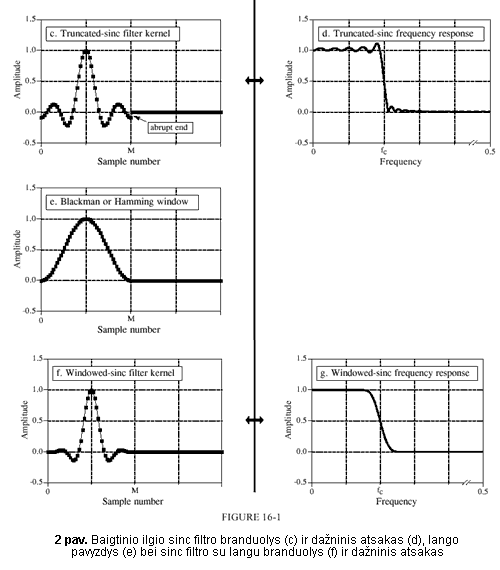
Apskritai galima naudoti įvairius langus (žiūr. 1 lentelę). Sunku pasakyti, kuris langas yra pats geriausias, kadangi bangavimas, užtvarinės srities slopinimas ir statumas yra tarpusavyje susiję: gerėjant vienam parametrui blogėja kitas. Dažniausiai naudojami Hammingo ir Blackmano langai. Hammingo langas duoda 20 % didesnį statumą nei Blackmano, tačiau Blackmano langas turi geresnį slopinimą užtvarinėje srityje. Be to, Blackmano filtras duoda 10 kartų mažesnį bangavimą praleidimo srityje.
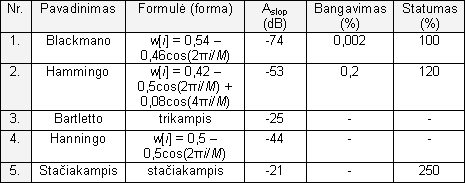
Geriausią slopinimą ir mažiausią bangavimą praleidimo srityje duoda Blackmano langas. Nors „sinc“ filtro su Hammingo langu statumas 20% didesnis už Blackmano, tačiau dažniausiai susidoroti su mažesniu statumu yra lengviau nei su didesniu bangavimu ir prastesniu slopinimu. Didžiausią statumą duoda stačiakampio langas, kuris praktiškai yra filtro branduolio kraštų nukirpimas, tačiau jis pasižymi ypatingai prastu slopinimu.
„Sinc“ filtro projektavimas
Norint suprojektuoti „sinc“ filtrą su langu reikia pasirinkti du parametrus: ribinį dažnį fc ir filtro branduolio ilgį M. Ribinis dažnis turi būti išreikštas kaip diskretizavimo dažnio trupmena ir turi būti intervale nuo 0 iki 0,5. M vertė apsprendžia filtro statumą (čia BW – perėjimo sritis tarp praleidimo ir užtvarinės srities):
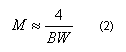
Perėjimo sritis BW, kaip ir ribinis dažnis, turi būti išreikštas kaip diskretizavimo dažnio trupmena ir turi būti intervale nuo 0 iki 0,5. Reikėtų paminėti, jog perėjimo sritis nepriklauso nuo ribinio dažnio.
Kadangi laikas, reikalingas konvoliucijai atlikti, proporcingas signalų ilgiui, (2) lygybė naudotina protingam vykdymo trukmės ir filtro statumo pasirinkimui. Pavyzdžiui Blackmano lango statumas yra 20 % mažesnis nei Hammingo, tačiau tai galima kompensuoti 20% ilgesniu branduoliu. Kitaip sakant, to paties statumo Blackmano langui reikia 20 % daugiau laiko nei Hammingo langui.
Parinkus fc ir M, filtro branduolį su Blackmano langu galime suskaičiuoti pagal šią lygybę (i – filtro branduolio taško indeksas):
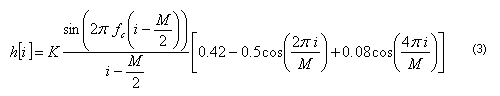
Svarbu paminėti, jog tam, kad tinkamai suskaičiuoti filtro branduolį, reikia parinkti konstantą K taip, kad filtro stiprinimas būtų lygus 1. Be to, tam kad išvengti dalybos iš nulio, taškui i = M/2, reikia priskirti tokią išraišką:
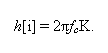
Sakykime, pasirinkome M = 100 (M turi būti lyginis). Pirmojo filtro branduolio taško indeksas yra 0, paskutiniojo – 101. Taigi filtro branduolio ilgis yra M+1. Simetrijos centras yra taške su indeksu 50, taigi 0 taško vertė turi būti lygi 100 taško vertei, o 45 taško vertė – 51 taško vertei.
Filtrų tipai. Filtrai skirstomi į žemo dažnio, aukšto dažnio, juostinius ir užtvarinius. Žemo dažnio filtras visus dažnius žemesnius nei ribinis praleidžia, aukštesnius - slopina. Aukšto dažnio filtras – atvirkščiai – visus dažnius, žemesnius už ribinį slopina, aukštesnius – praleidžia. Juostinis filtras turi du ribinius dažnius, jis praleidžia visus dažnius, esančius tų dviejų ribinių dažnių intervale, o slopina visus dažnius, esančius už šio intervalo. Tuo tarpu užtvarinis filtras, priešingai nei juostinis, visus dažnius iš intervalo slopina, o likusius – praleidžia.
Iš esmės projektuojami tik žemo dažnio filtrai, likusiųjų filtrų tipai gaunami iš žemojo dažnio filtro. Aukštojo dažnio filtrą iš žemojo galime gauti dviem būdais: spektrine inversija ir spektrine reversija. Spektrinę inversiją filtrui atlikti yra labai paprasta:
- Visus žemojo dažnio filtro branduolio taškus pakeičiame į priešingo ženklo.
- Pridedame vienetą prie simetrijos centro taško.
Aukštojo dažnio filtrą galime gauti ir spektrinės reversijos būdu: tereikia pakeisti kas antro žemojo dažnio filtro branduolio taško ženklą. Šis veiksmas tolygus branduolio daugybai iš sinusoidės, kurios dažnis 0,5. Praktiškai toks veiksmas perslenka dažnio sritį per 0,5, o neigiamieji dažniai intervale (–0,5; 0) yra veidrodinė kopija teigiamų dažnių (0; 0,5).
Norėdami gauti užtvarinį filtrą, turėtume sudėti panariui žemojo dažnio filtro branduolį ir aukštojo dažnio filtro branduolį.
Norėdami gauti juostinį filtrą, turėtume spektrinės inversijos ar reversijos būdu invertuoti užtvarinį filtrą arba sukonvoliuoti aukštojo ir žemojo filtro branduolius.
„Sinc“ filtro pranašumas. Sinc filtrai su langu turi vieną labai didelį pranašumą prieš kitus filtrus – jų parametrus galima gerinti iki begalybės. Be abejo, tai yra atliekama vykdymo laiko sąskaita, tačiau ten, kur filtro parametrai vaidina didžiausią vaidmenį, „sinc“ filtras su langu yra nepakeičiamas.
Pavyzdžiui, jei norėtume išskirti 0,1 mV signalą iš 60 V telefono linijos, mums reikėtų filtro, kuris užtvarinę sritį slopintų bent -135 dB. Praleidus šį signalą pro „sinc“ filtrą su Blackmano langu du kartus, užtvarinę sritį užslopinsime net –148 dB. Be abejo, daugkartinis praleidimas pro filtrą truputėlį pablogina statumą, tačiau gaunamas slopinimas yra neįtikėtinas.
„Sinc“ filtro trūkumai. Minėtasis „sinc“ filtro pranašumas yra ir trūkumas, kadangi kuo geresnius filtro parametrus norime gauti, tuo daugiau laiko reikia konvoliucijai atlikti.
Grįžtant prie pateiktojo pavyzdžio, negalima nepastebėti, kad „sinc“ filtro parametrai iš tikrųjų yra įspūdingi, nes neįmanoma net įsivaizduoti tokio analoginio filtro, kuris galėtų užtvarinę sritį slopinti –148 dB ar net daugiau. Tačiau toks platus įtampų diapazonas įneša labai didelius reikalavimus pačiam signalo įrašymui bei apdorojimui. Kompiuteryje standartiškai naudojamo viengubo tikslumo slankaus kablelio skaičiaus (angl. single precision floating point number) jau nelabai užtenka, kadangi apvalinimo paklaida sudarys triukšmą apie –150 dB. Be to, jei norėtume užregistruoti tokio plataus diapazono įtampą, turėtume naudoti bent 22 bitų tikslumo analoginį – skaitmeninį keitiklį. Nors tokį keitiklį rasti galima, tačiau jo registravimo dažnis neviršys kelių dešimčių hercų. Nepaisant to, kad visi registruojančios schemos elementai turėtų būti ypatingai preciziški, o triukšmai sumažinti iki maksimumo.
„Sinc“ filtro nauda. „Sinc“ filtras su langu yra labai tinkamas naudoti tokiais atvejais, kai svarbiausias reikalavimas filtrui yra jo parametrai ir galima nekreipti dėmesio į vykdymo laiką. Jei filtro parametrai nėra kritiški, galima pasirinkti kitokį filtrą, kuris suteiks panašią kokybę, tačiau trumpesnį vykdymo laiką.
Sanklodų sudėties metodas
Kai filtro branduolys jau sugeneruotas, belieka sukonvoliuoti signalą su branduoliu ir džiaugtis rezultatais. Tačiau ir čia viskas ne taip paprasta, kadangi susiduriame su problema – praktikoje labai dažnai susiduriame su signalais, kurie yra labai ilgi, ir jie tiesiog netelpa į kompiuterio atmintį. Net jei ir tilptų, problema išlieka, kadangi dažnai susiduriame su situacijomis, kur signalus reikia apdoroti realiame laike, t. y. signalo ilgis begalinis.
Problemai spręsti panaudosime sanklodų sudėties metodą (žiūr. 3 pav.) Jo esmė tokia – suskaidome signalą segmentais, kiekvieną segmentą konvoliuojame su filtro branduoliu, o rezultatus sudedame. Viskas atrodo labai gražu, tačiau tenka prisiminti vieną smulkmeną apie konvoliuciją. Jei turime M taškų signalą ir N taškų branduolį, juos sukonvoliavę gausime M+N-1 taškų signalą. Todėl tiesiog karpyti signalą ir sudėti rezultatus nepavyks, priešingu atveju, gautume logikai prieštaraujantį teiginį, kad apdorotame signale atsiranda daugiau informacijos, nei pradiniame.
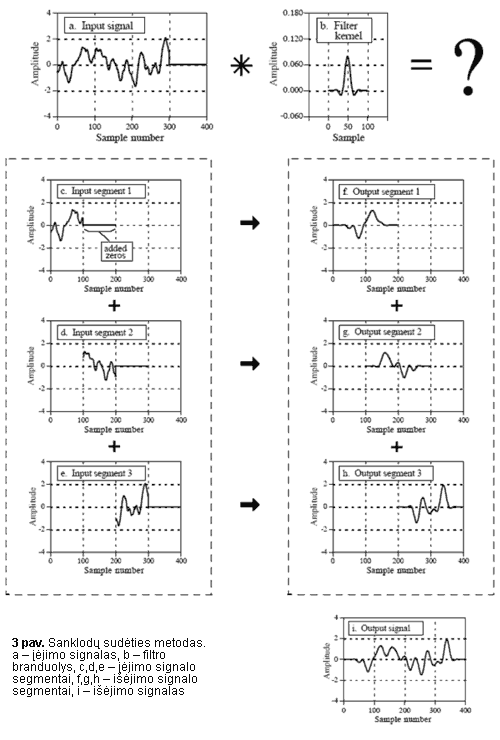
Vieną įėjimo segmentą iš N taškų turi sudaryti N/2 įėjimo signalo ir N/2 taškų, užpildytų nuliais. Tokį segmentą turime konvoliuoti su M taškų filtro branduoliu, kurio M/2 taškuose yra pats filtro branduolys, o kituose taškuose – nuliai. Tokius išėjimo signalo segmentus turime sudėti ir gausime išėjimo signalą. Beje, išėjimo signale M/2 taškų pačioje pradžioje ir M/2 pačioje pabaigoje bus sugadinti, juose bus klaidinga informacija.
Sanklodų sudėties leidžia paprastai filtruoti labai ilgus signalus, apdoroti signalus realiame, be to, be šio metodo nelabai įmanoma pasinaudoti FFT konvoliucija.
FFT konvoliucija
Standartinė konvoliucija yra gana sudėtinga ir užima gana daug laiko, kurio ir taip visada trūksta. Kaip žinome, konvoliucija laiko srityje yra ekvivalenti daugybai dažnio srityje. Todėl filtruoti galime ne tik konvoliuodami įėjimo signalą su išėjimo signalu, bet ir tokiu būdu:
- Atlikti Furjė transformaciją įėjimo signalui.
- Atlikti Furjė transformaciją filtro branduoliui.
- Panačiui sudauginti šiuos masyvus.
- Atlikti atvirkštinę Furjė transformaciją.
- Pakoreguoti išėjimo signalo amplitudę (padauginti iš šaknies iš N).
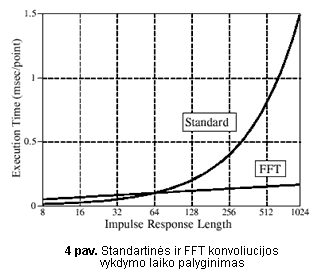
Nors aprašytasis metodas atrodo daug sudėtingesnis, tačiau jei Furjė transformaciją ir atvirkštinę Furjė transformaciją atliktume pagal FFT (Fast Fourier Transform) algoritmą, ilgesnių nei 60 taškų signalų konvoliuciją galėtume žymiai pagreitinti (žr. 4 pav.). Konvoliucija, kuri yra atliekama tokiu būdu yra vadinama sparčiąja konvoliucija arba tiesiog FFT konvoliucija.
Praktinis „sinc“ filtro su langu panaudojimas ir analizė
„Mathcad“ programa (sinc_filter.mcd) buvo parašytas užtvarinis „sinc“ filtras su langu (dažniai 0,22 ir 0,33) ir pabandyta juo apdoroti dirbtinį signalą. Konvoliucija buvo atliekama sanklodų sudėties bei sparčiosios Furjė transformacijos metodais. Signalas buvo sudarytas iš trijų sinusoidžių, dvi iš jų buvo didesnių amplitudžių nei trečioji, filtras turėjo šias dvi sinusoides pašalinti. „Sinc“ filtrui dėl savo universalumo buvo parinktas Blackmano langas.
Filtravimas iš esmės pavyko, kaip matyti iš paskutiniojo grafiko (žiūr. priedą 1), filtras sėkmingai nufiltravo pašalintinus dažnius, nors maži pikiukai spektre dar matyti.
Labai svarbu išėjimo signale nukirpti pirmuosius M/2 ir paskutinius M/2 taškus (M – filtro branduolio ilgis), kadangi šie taškai įneša tik triukšmą, todėl gaunamas neteisintas spektras.
Išvados
Išnagrinėtasis „sinc“ filtras yra puiki priemonė dažniams atskirti, jo parametrus praktiškai riboja tik paties įėjimo signalo triukšmai bei vykdymo laikas. Praktiškai išnagrinėtas „sinc“ filtras su Blackmano langu buvo puiki priemonė darbo autoriui praktiškai susipažinti su filtro projektavimu ir įgyvendinimu.
Literatūra
- Smith S.W. The Scientist and Engineer’s Guide to Digital Signal Processing. Second Editon.– San Diego, California, – 1999. www.dspguide.com.
- Scherz P. Practical Electronics for Inventors. – McGraw-Hill. – 2000.
Straipsnį kartu su „Mathcad“ programa galite atsisiųsti iš archyvo.
