Idealaus rezistoriaus varžos modelis
Laidininkų varža. Laidininko dalies varža priklauso nuo laidininko medžiagos, nuo jo matmenų ir formos. Pasirodo, kad pastovaus skerspjūvio S ir ilgio l laidininko atkarpos varža yra lygi:
R=r*l/S
čia r – dydis, priklausantis tik nuo laidininko medžiagos, jis vadinamas medžiagos specifine varža. Tuo būdu, laidininko atkarpos varža tiesiog proporcinga jos ilgiui l ir atvirkščiai proporcinga jos skerspjūvio plotui S. Iš formulės turime: r=R*S/l, kur matyti, kad specifinė varža r skaitmeniškai lygi laidininko ,turinčio vienetinį ilgį ir skerspjūvio plotą, lygų ploto vienetui. CGSE sistemoje varžos vienetu laikoma varža laidininko, kuriuo, kai galų potencialų skirtumas yra vienas CGSE vienetas, teka vieno CGSE vieneto stiprumo srovė. Kadangi šis vienetas praktiniams reikalams per didelis, tai praktiniu varžos vienetu yra paimta varža laidininko, kuriame atsiranda vieno ampero srovė, kai potencialų skirtumas yra vienas voltas. Šis vienetas vadinamas omu ir žymimas W. Ryšį tarp omo ir varžos CGSE vieneto gausime, pasinaudodami sąryšiu, išplaukiančiu iš Omo dėsnio: 1omas=1 voltas/1 amperas=1/300 potencialo CGSE vieneto/3*109 srovės stiprumo CGSE vienetų =1/9*1011 varžos CGSE vieneto. Milijonas omų yra vadinamas megomu. Varžos dimensija gausime remdamiesi lygybe: [R] =[V]/[A] =TL-1.
Specifinę varžą r praktinėje sistemoje įprasta matuoti vienetais, nustatomais remiantis jos formule, išreiškiant varžą R omais, skerspjūvio plotą S – kvadratiniais centimetrais, o ilgį – centimetrais, gautasis specifinės varžos vienetas – omas-centimetru (Wcm). Tuo būdu, specifinės varžos vienetu laikoma specifinė varža tokios medžiagos, iš kurios pagamintas kubas su 1cm ilgio briauna turi 1 W varžą, kai srovė teka nuo to kubo vienos sienos prie priešingos sienos. Be specifinės varžos r, dažnai įvedamas atvirkščias dydis: σ=1/ r, vadinamas specifiniu laidumu arba elektros laidumu. Specifinė varža priklauso nuo laidininko temperatūros. Beveik visų metalų specifinė varža įprastoje temperatūroje kinta tiesiškai, priklausydama nuo temperatūros: r=r0(1+αt), čia t – temperatūra pagal Celsijaus skalę, r0 –specifinė varža esant 0ºC, α – pastovus koeficientas.
Kai kurių laidininkų specifinė varža ir elektros laidumas 0ºC temperatūroje:
| Laidininkas | r, Wcm | σ,1/Wcm |
|---|---|---|
| Aliuminis | 2,53*10-6 | 39,5*104 |
| Grafitas | 39,2*10-6 | 2,55*104 |
| Geležis, gryna | 8,69*10-6 | 11,48*104 |
| Varis, grynas | 1,55*10-6 | 64,5*104 |
| Gyvsidabris | 94,3*10-6 | 1,06*104 |
Daugeliui metalų α skaitmeninė vertė yra artima 0,00367, t. y., 1/273. Taigi, r užrašoma taip: r= αr0T, kur T – temperatūra pagal absoliutinę skalę. Tačiau šis sąryšis yra apytikrio pobūdžio ir nepasiteisina nei aukštoje, nei labai žemoje temperatūroje. Aukštoje temperatūroje α didėja.
Be to, varža padidėja metalams lydantis. Žemoje temperatūroje α mažėja. Labai žemoje temperatūroje (1–7º pagal absoliutinę skalę) kai kurių metalų ir lydinių varža staigiai mažėja iki labai mažo dydžio. Šis reiškinys, pirmą kartą atrastas olandų fiziko Kamerling-Oneso 1911m.,vadinamas superlaidumu. Praktiškai varža superlaidumo atveju lygi nuliui. Dabar yra nustatytas daugelio grynų metalų ir tų metalų elementų tarpusavio lydinių bei jų lydinių su kitais elementais superlaidumas.
Superlaidumo būsena išnyksta esant, veikiant kelių šimtų estedų magnetiniam laukui. Pastaruoju metu superlaidumą teoriniu ir eksperimentiniu požiūriu labai smulkiai ištyrė fizikai L. D. Landau, A. I. Šalnikovas ir kt. Šalnikovas pastebėjo, kad laidininke, kai jis pereina iš superlaidumo būsenos į paprastąją, susidaro atskiri superlaidūs sluoksniai, besikaitaliojantieji su paprastais sluoksniais. Bet vis dėlto išsamios informacijos apie superlaidumą iki šiol nėra. Be metalų, kurie yra labai geri laidininkai, yra kūnų su daug mažesniu laidumu, pvz. selenas, vienvalenčio vario oksidas ir kt. Tie kūnai vadinami puslaidininkiais. Puslaidininkiai skiriasi nuo metalų ne tik žymiai mažesniu laidumu, bet ir kitokia σ priklausomybe nuo temperatūros. Jei metalų atveju σ mažėja, didėjant temperatūrai, tai puslaidininkių atveju jis, didėjant temperatūrai, didėja pagal dėsnį:
σ= σ0 *e-b/T
kur T – absoliutinė temperatūra, o b – konstanta, skirtinga įvairiems puslaidininkiams. Kai kurių puslaidininkių susilietimo su metalais vietoje pastebimi ypatingi reiškiniai: susidaro užveriamasis sluoksnis, praleidžiantis srovę tik viena kryptimi. Pvz., vienvalenčio vario oksido atveju elektros srovė yra tūkstančius kartų didesnė, kai ji teka nuo metalo į vario oksidą, negu atvirkščia kryptimi. Šis reiškinys sudaro šiuolaikinių kietųjų kintamosios srovės lygintuvų konstrukcijos pagrindą. Elektrinių jėgų darbo, pernešant krūvį, ryšys su laidininko varža: A=I²Rt. Šilumos kiekio sąryšis su varža toks: Q=0,24 I²Rt. Tai Lenco-Džaulio dėsnis. Kuo mažesnė laidininko specifinė varža, tuo mažesnis šilumos kiekis (esant tokiai pat srovei) jame išsiskiria. Superlaidumo būsenoje, kai specifinė varža pasidaro neišmatuojamai maža ,tekant srovei laidininke, neišsiskiria bent kiek pastebimo šilumos kiekio. Kadangi šiuo atveju srovės energija niekur neeikvojama, tai uždarame superlaidininke srovė, kartą sužadinta, teka neribotai ilgai, neeikvodama energijos iš išorės.
Nuosekliame jungime bendroji varža lygi R=R1+R2 +…ir Q1/Q2=R1/R2. Lygiagrečiai sujungus bus taip 1/R=1/R1+1/R2+…,o I1/I2=R2/R1 bei Q1/Q2=R2/R1.
Grandinės varžai keisti naudojami prietaisai – rezistoriai. Laboratorinėje praktikoje nedidelėms srovėms naudojami stumdomo kontakto rezistoriai – reostatai. Tokį rezistorių sudaro viela, apvyniota ant porcelianinio cilindro. Stumdant kontaktą, galima keisti įjungiamų į grandinę vielelės vijų skaičių, o tuo pačiu ir įjungiamos varžos didumą. Vielelė daroma iš lydinių, turinčių gana aukštą specifinę varžą ir mažą temperatūrinį koeficientą. Silpna varžos priklausomybė nuo temperatūros reikalinga tam, kad nuo srovės kaistančio rezistoriaus varža pastebimai nepakistų. Tokie rezistoriai labai patogūs, tačiau jų konstrukcija negarantuoja pakankamai gero šilumos atidavimo, o dėlto jie stipriai įkaista, ir jais negalima naudotis, kai turime reikalą su stipriomis srovėmis. Didelėms srovėms naudojami rezistoriai, pagaminti iš storų vielų, suvyniotų į spirales. Laidininko varžą lengvai galima išmatuoti ampermetru ir voltmetru.
Standartinės varžos paprastai gaminamos vadinamųjų kištukinių rezistorių pavidalo, t. y. rezistorių sudaro eilė ričių. Viso grandinėje išsiskiriančio galingumo priklausomybė nuo varžos atrodys taip:W=Iε=ε²/R+R0 t. y. didėjant R, galingumas krinta, asimptotiškai artėdamas prie nulio, neribotai didėjant R. Uždaroje grandinėje visa varža susideda iš išorinės grandinės dalies varžos R ir vidinės grandinė dalies varžos R0, iš čia
I=ε/ R+R0 .
Omo dėsnis, jo diferencialine išraiška. Omo dėsnis visai grandinei
Sujunkime paprasčiausią elektros srovės grandinę ( 14.2 pav.) , kurioje E yra elektros srovės šaltinis, V – voltmetras, A – ampermetras, R – varžynas. Voltmetras, įjungtas tarp taškų M ir N, rodo grandines dalies MARN įtampą U, o ampermetras – nuolatines srovės stiprumą I. Kiek kartų padidiname Įtampą U tarp taškų M ir N, įjungdami į grandinę naujus elektros srovės šaltinius, tiek pat kartų toje pačioje grandines dalyje MARN padidėja ir srovės stiprumas I. Remdamasis bandymais, G. Omas nustatė tarp įtampos U ir sroves stiprumo tokį ryšį: U=RI; čia įrašytas proporcingumo koeficientas R tai pačiai grandines daliai MARN yra pastovus ir vadinamas elektrine varža. Šiuo metu Omo dėsnį priimta rašyti šitokia forma:
U=IR.
Įtampa tarp grandinės dalies MARN galų yra lygi srovės stiprumo ir grandinės dalies varžos sandaugai. Sandauga IR vadinama įtampos kritimu varžoje R.
Dažnai Omo dėsnis išreiškiamas formule
I=U/R
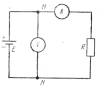
t. y. srovės stiprumas duotoje grandinės dalyje MARN yra tiesiog proporcingas įtampai tarp jos galų ir atvirkščiai proporcingas tos grandinės dalies varžai R.
Išreiškę Omo dėsnį pavidalu
R=U/I
įrašę U=1 V, I=1 A, gauname R=l W. Omas yra varža tokio laidininko, kuriuo teka 1 A stiprumo srove, kai tarp jo galų yra 1 A stiprumo srovė, kai tarp jo galų yra 1V įtampa. Kartais teoriniuose skaičiavimuose naudinga taikyti Omo dėsnį be galo mažoms grandines dalims. Sakykime, ilgio 1 ir pastovaus skerspjūvio S vienalyčiu laidininku teka nuolatine srove I. Tada, įrašę į Omo dėsnio grandinės daliai formulę varžos vertę iš formulės ir pertvarkę, gauname:
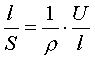
Santykis
![]() yra elektros sroves tankis,
yra elektros sroves tankis,
![]() -
specifinis laidumas,
-
specifinis laidumas,
![]() – vienalyčio elektrinio lauko stiprumas išilgai ilgio 1 laidininko; ilgis 1 čia gali kiek norint mažėti ir laido atkarpa gali virsti be galo maža. Taigi j=gE. Kadangi, tekant srovei, teigiamų krūvių judėjimo kryptis sutampa su elektrinio lauko stiprumo kryptimi, tai elektros srovės tankio vektoriaus j kryptis sutampa su elektrinio lauko stiprumo vektoriaus E kryptimi. Šie abu vektoriai bet kuriame laidininko taške yra vienas kitam tiesiog proporcingi:
– vienalyčio elektrinio lauko stiprumas išilgai ilgio 1 laidininko; ilgis 1 čia gali kiek norint mažėti ir laido atkarpa gali virsti be galo maža. Taigi j=gE. Kadangi, tekant srovei, teigiamų krūvių judėjimo kryptis sutampa su elektrinio lauko stiprumo kryptimi, tai elektros srovės tankio vektoriaus j kryptis sutampa su elektrinio lauko stiprumo vektoriaus E kryptimi. Šie abu vektoriai bet kuriame laidininko taške yra vienas kitam tiesiog proporcingi:
j=gE
Tai ir yra Omo dėsnio diferencialinė išraiška.
Grandinės dalies galų įtampa lygi potencialų skirtumui tik tuo atveju, jei toje grandines dalyje evj E=O; kitaip sakant, toje grandines dalyje neturime elektros sroves šaltinio.
Kirchhofo taisyklės
Išsišakojusioje grandinėje tekančių srovių stiprumą paprasčiausia skaičiuoti naudojantis dviem G. Kirchhofo nustatytomis taisyklėmis.
Pirmoji Kirchhofo taisykle: į išsišakojusios grandinės mazgą įtekančių ir iš jo ištekančių elektros srovių algebrine suma lygi nuliui.
Išsišakojusios grandines mazgu vadiname bet koki tašką, į kurį sueina daugiau kaip du laidai. Jei, pavyzdžiui, į grandines mazgą A įteka elektros srovės, kurių stiprumai I1, I2, I3, o išteka srovės I4, I5, tai
arba
Ši taisyklė reiškia, kad ne viename elektros srovės grandinės taške negali kauptis elektra, t. y. koks elektros krūvis ateina į kurį nors tašką, toks turi ir iš jo išeiti.
Antroji Kirchhofo taisykle: išsišakojusios elektros srovės grandinės bet kurio uždaro kontūro šakomis tekančių elektros srovių Ik ir atitinkamų varžų Rksandaugų algebrine suma yra lygi to kontūro elektrovaros jėgų Ek algebrinei sumai.
Išsišakojusią grandinę sudaro atskiri uždari kontūrai. Sakykime, uždaro kontūro ABC atskiromis šakomis tekančių srovių stiprumai yra I1, I2, I3 o jų varžos R1, R2, R3. Kiekvieno atskiro uždaro kontūro apėjimo kryptį pasirenkame laisvai. Jei apėjimo kryptis išorinėje grandinėje sutampa su srovės kryptimi, tai sandauga IkRk laikoma teigiama, o priešinga kryptis laikoma neigiama. Jei, apeinant išorinę grandinę, srovės šaltinis praeinamas kryptimi iš katodo į anodą, tai jo evj Ek laikoma teigiama, o priešinga kryptimi – neigiama. Visam uždaram kontūrui ABC, kurio apėjimo kryptis pasirinkta prieš laikrodžio rodyklės judėjimą, antroji Kirchhofo taisyklė užrašoma taip:
arba
Elektros srovės darbui ir energijai apskaičiuoti prisiminkime formulę, pagal kurią, laidininku praėjus elektros krūviui Q atliekamas darbas:
A=QU;
čia U yra įtampa tarp laidininko galų. Įrašę Q išraišką iš formules, gauname nuolatinės elektros srovės atliktą darbą:
A = Ult
Iš Omo dėsnio įrašę U =IR, gauname kitą elektros srovės atlikto darbo išraišką:
A =I2Rt.
Padaliję elektros srovės darbą iš laiko per kuri jis atliekamas gauname sroves galią:
p= UI= I2R.
Elektros srovės atliktas darbas A yra tolygus elektros srovės suvartotai energijai W, t. y. A=W.
Elektrolito omine varža vadinama vidine elemento varža. Pažymėkime elemento pašalinę evj e, išorinės grandinės varžą R ir elemento vidinę varžą r. Omo dėsnį visai grandinei tada užrašysime šitaip:
e=I(R +r).
Elemento evj priklauso nuo to elemento savybių ir nepriklauso nuo grandine tekančios sroves stiprio. Iš formules matyti, kad įtampos kritimas išorinėje grandinėje (U=IR) nelygus elemento elektrovaros jėgai ir visada už ją mažesnis. Tai yra įtampa tarp veikiančio elemento gnybtų, kai grandine teka srove. Srovei stiprėjant, įtampa išorinėje grandinėje mažėja, ir juo labiau, juo didesne vidine elemento varža. Naudojant elementą visada pageidautina, kad įtampa išorinėje grandinėje kuo mažiau priklausytų nuo srovės stiprio, t. y. nuo apkrovos. Todėl svarbus elementą l apibudinantis dydis yra vidinė varža. Juo ji mažesne, juo geresne yra pasalinių evj šaltinio kokybe, jei kitos sąlygos vienodos.
Džaulio ir Lenco dėsnio diferencialinė išraiška. Srovės atliekamas darbas ir pasiekiama galia
Srovės darbas. Galia. Jeigu tarp dviejų tašku, kurių potencialų skirtumas lygus U, yra pernešamas krūvis dQ, tai atliekamas darbas.
dA = U dQ
Tarkime, kad laidininku teka I – stiprio srovė. Per laiką dt ta atkarpa, tarp kurios galų yra potencialų skirtumas U, pratekės krūvis dQ = I dt ir bus atliktas darbas.
dA = IU dt
toje atkarpoje srovės galia P=dA/dt=IU
Išsiskiriančios energijos rūšis priklausys nuo potencialo kritimą sąlygojančių fizikinių priežasčių kilmės. Dėl potencialo kitimo ominėje varžoje išsiskiria šiluma. Dėl potencialo kitimo tarp nuolatinės srovės variklio gnybtų atliekamas mechaninis darbas ir t. t. Formule išreiškiama maksimali srovės galia, pasiekiama atkarpoje, kurioje potencialas krinta dydžiu U. Jei potencialas krinta tik dėl laidininko omines varžos, tai pagal Omo dėsnį U=IR; R – tos atkarpos varža. Tada visa energija išsiskiria šilumos pavidalu. Ir atitinkama galia
P = IU =I2R
Ši formulė vadinama Džaulio ir Lenco dėsniu.
Šakotinės grandinės. Praktikoje grandinės dažniausiai būna sudėtingesnės, kaip, pavyzdžiui, pav. Tačiau bet kokią sudėtingą grandinę sudaro dviejų rūšių paprasčiausi elementai:
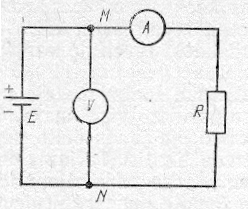
2 pav.
1) mazgai, į kuriuos sueina daugiau kaip du laidai (2 pav., C ir D taškai);
2) uždari kontūrai (2 pav., ABDCA, CDFEC, ABFEA kontūrai).
Kirchhofo dėsniai. Kirchhofo dėsniai naudojami sudaryti lygčių sistemoms, kurias išsprendus randami bet kokio sudėtingumo šakotinės grandinės stipriai. Tos lygtys yra kiekvienam uždaram kontūrui užrašytas Omo dėsnis ir krūvio tvermės dėsnis kiekviename mazge. Srovės stiprių ir evj ženklų taisyklės kiekvieno uždaro kontūro tokios pat, kaip ir izoliuoto kontūro. Visų kontūrų teigiamo apėjimo kryptis parenkama ta pati. Krūvio tvermės dėsnis reikalauja, kad visų į mazgą įtekančių srovių stiprių suma būtų lygi iš mazgo ištekančių srovių stiprių sumai. Kitaip sakant, visų per mazgą tekančių srovių stiprių algebrinė suma turi būti lygi nuliui. Užrašant srovių stiprių sumą, iš mazgo išeinančiomis strėliukėmis pažymėti stipriai rašomi, pavyzdžiui, su minuso ženklu, o į mazgą sueinančiomis strėliukėmis – su pliuso ženklu. Žinoma, galima imti ir priešingus ženklus, tai nepakeis atitinkamų lygčių, tik svarbu visuose mazguose laikytis tos pačios taisyklės.
Taigi Kirchhofo dėsniai formuluojami šitaip:
1) visų per mazgą tekančių srovių stiprių algebrinė suma lygi nuliui:
2) kiekvieno uždaro kontūro atskirų dalių srovės stiprių verčių ir atitinkamų dalių varžų sandaugų suma yra lygi tame kontūre esančių pašalinių evj algebrinių verčių sumai:
Galima įrodyti, kad taip sudarytų bet kokios šakotinės grandinės lygčių sistema yra pilna ir, ją išsprendus, galima surasti visų srovių stiprius.
Tuos dėsnius išvedė Kirchhofas (G. Kirchhoff, 1824–1887), 1847 m. jis parodė, kaip bendruoju atveju reikia spręsti nuolatinės srovės šakotinių grandinių uždavinį, nors pačius dėsnius suformulavo jau 1845 m.
Pasinaudosime Kirchhofo dėsniais 2 paveiksle pavaizduotos grandinės uždaviniui spręsti.
Pagal pirmąjį Kirchhofo dėsnį:
a) –I1-I2-I3=0 (C mazgas);
b) I1+12+13=O (D mazgas)
Pagal antrąjį Kirchhofo dėsnį.
a) I1 r1 +I1 R1-I2 R2-I2 r2=ε1+ε2 ;
b) I2 R2+I2 r2-I3 R3-I3 r3= -ε2-ε3;
c) I1r1+I1R1-I3R3-I3r3=ε1-ε3 .
Čia rl, r2, r3- pašalinių evj šaltinių vidinės varžos. Mazgų lygtys viena su kita sutampa, o iš trijų kontūrų lygčių nepriklausomos yra tik dvi. Pavyzdžiui, panariui sudėję pirmąsias dvi, gauname trečiąją. Taigi yra trys lygtys su trimis nežinomaisiais – srovių stjpriais I1, I2,13. Išsprendę tą lygčių sistemą, rasime srovių stiprius ir tikrąsias jų kryptis. Bet dar neišsprendę galime teigti, kad 2 paveiksle apsirikome žymėdami srovių kryptis, nes, taip parinkus kryptis, mazguose nebūtų išlaikytas krūvio tvermės dėsnis – C mazge turėtų kauptis neigiamas krūvis, o D mazge – teigiamas. Bet dėl to mums nėra ko rūpintis, nes iš sprendinio ir taip pamatysime, kokios turi būti tikrosios srovių kryptys.
Iš pateiktojo pavyzdžio matome, kad įrašę visų kontūrų ir visų mazgų Kirchhofo lygtis, turime daugiau lygčių negu reikia, nes ne visos lygtys yra nepriklausomos. Nenorint apsunkinti darbo, pageidautina nereikalingų lygčių nerašyti. Rekomenduotina naudotis tokia taisykle. Rašant eilinę uždaro kontūro lygtį reikia žiūrėti, kad nors vienas jos narys turėtų dydį, kurio dar nebuvo prieš tai parašytose lygtyse; jei visi dydžiai buvo jau ankstesnėse lygtyse, tai šita lygtis jau nebereikalinga. Panašiai elgiamės ir rašydami mazgų lygtis.
