Maždaug 300 metų prieš Kristaus gimimą, to meto astronomai, galvodami, kad Saulė sukasi aplink Žemę apskritimu, pasiūlė apskritimą padalinti į 360 dalių, o vieną jo dalį pavadino laipsniu. Pavyzdžiu tam buvo metai, kurie sudarė 365,25 dienas.
Maždaug tuo pačiu laiku Euklidas parašo knygą „Pradmenys“, kurioje išdėsto geometrijos pagrindus. Jo knyga buvo leidžiama apie 2000 metų ir išleistų knygų skaičiumi atsiliko tik nuo Biblijos. Maždaug tuo laiku Pitagoras nagrinėdamas trikampį, suformuoja teoremą, kuria dažnai naudojamės ir dabar.
Toliau nagrinėdami trikampį, to meto matematikai, pasiūlo stačiakampio trikampio dviejų kraštiniu ilgio santykius pavadinti atskirais vardais. Ir tie vardai buvo sin, (lot. sinus – išlinkimas) cos, tg, ir ctg. Nustatyta, kad tie santykiniai dydžiai priklauso nuo kampų dydžių. Ta priklausomybė buvo suvesta į lenteles, kuriomis buvo naudojamasi šimtmečiais (kartai naudojamos ir dabar). Tie santykiniai dydžiai pavadinti funkcijomis. Jeigu tai funkcijos, tai jos turėtų turėti analitines išraiškas nuo kampo dydžio. Tai leistu, ištisas knygas su lentelėmis pakeisti keliomis formulėmis. Tačiau ilgai nepavykdavo surasti šių funkcijų analitinių išraiškų. Tik Euleris sugalvojo būdą kaip šių funkcijų priklausomybes išreikšti begalinėmis eilutėmis. Tiesa, tada tradicinis kampo dydis matuojamas laipsniais, minutėmis ir sekundėmis turi būti perskaičiuojamas į radianus.
Radianas – tai apskritimo lanko, atitinkančio kampą, ilgis. Taigi ir šiandiena, norėdami suskaičiuoti sinα, cosα, tgα ar ctgα naudojamės Eulerio pasiūlytomis begalinėmis eilutėmis, o eilutės argumentas yra apskritimo lanko ilgis. Skaičiuojamos eilutės narių skaičių pasirenkame tokį, kokiu tikslumu mums reikia skaičiuoti funkcijų reikšmes.
Pavyzdžiui geodezijoje, taško ant Žemės elipsoidinio paviršiaus padėtį reikia skaičiuoti dešimtųjų ar šimtųjų sekundės dalių tikslumu. O tai reiškia, kad skaičiavimai turi būti atliekami vienos dešimt milijoninės dalies tikslumu (aštuonių ženklų dešimtainėje sistemoje tikslumu). Kita ne mažiau aktuali skaičiavimo problema yra ta, kad po to, kai apskritimas padalinamas į 360 laipsnių, vienas laipsnis padalinamas į šešiasdešimti minučių, o viena minutė – į šešiasdešimti sekundžių. Tokiu būdu susidaro neįprastos skaičiavimo sistemos. Dabar, praktikoje daugiausia naudojamos yra dešimtainė ir dvejetainė skaičiavimo sistemos.
Kita, šios istoriškai susiklosčiusios Euklido geometrijos, o kartu ir kampo trigonometrijos apskritime taikymo problema yra ta, kad įvairiuose taikomojo pobūdžio skaičiavimuose (pav., teorinėje mechanikoje, mašinų ir mechanizmų teorijoje, aerodinamikoje ir kitur), nei pradinėse sąlygose nei suskaičiuotuose parametruose kampo išvis nėra. Tačiau sudarant šių sistemų matematinius modelius, naudojamasi tradiciniais matematiniais metodais, būtinai figūruoja sin,cos, tg, ctg . Tokiu atveju būtina įsivesti (susiskaičiuoti) kampus, bei kampo trigonometrines funkcijas tiktai tam, kad galima būtų pasinaudoti tradiciškai susiklosčiusius matematinius modelius.
Visą tai privertė galvoti, ar nėra kitų būdų sudaryti fizinių objektų matematinius modelis, kad išvengtume aukščiau minėtų problemų. Nagrinėjant trigonometrijos, kaip geometrijos mokslo dalies teorijos problemas, iškilo klausimas, kodėl yra sinusas apskritime (sin), yra sinusas hiperbolinis (sh), bet nėra sinuso parabolinio. Pasirodė, kad toks parabolinis sinusas gali būti.
1987m. Vilniaus universitete įvykusioje matematikų konferencijoje, kurios organizatoriais buvo ir Lietuvos mokslų akademijos Matematikos ir kibernetikos institutas, perskaičiau pranešimą „Kur dingo parabolinis sinusas“, kuriame ir buvo pasiūlyta įsivesti parabolinį sinusą sph, parabolinį kosinusą cph ir parabolinį tangentą tph, kuriuose skirtingai nei klasikinėse trigonometrijos funkcijose, kampo dydžio matuojamo laipsniais nėra. Vietoje kampo dydžio α (alfa), naudojama trikampio aukštinė – h. sph, cph ir tph yra algebrinės funkcijos. Šis pranešimas paskelbtas aukščiau minėtos konferencijos darbuose, bei kai kuriuose Kijeve ir Maskvoje leidžiamuose žurnaluose. Šių funkcijų išraiškos, su kai kuriais jų taikymo pavyzdžiais buvo pateiktos mano straipsniuose (D. Zanevičius, „Neosinusai elektrotechnikoje ir mechanikoje“, Lietuvos mokslų akademijos ir Lietuvos inžinierių sąjungos žurnale „Mokslas ir technika“ 2006 Nr. 1 ir „Neosinusai 2“ – „Mokslas ir technika“ 2007 Nr. 2)
2007 m. leidykla „Ciklonas“ išleido Donaldo Zanevičiaus knygą:
„h – geometrija. Neosinusų naudojimas skaičiavimams“
Knyga moksleiviams, studentams, mokytojams ir dėstytojams.
Funkcijos sph ir cph apibrėžiamos:
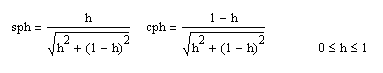
Pateiksiu kelias h-geometrijos ir jos funkcijų sph ir cph principines nuostatas ir jų (funkcijų) sulyginimą su klasikine trigonometrija, kuri yra klasikinės geometrijos dalis.
Prieš tai, keletą sakinių apie matematikos taikymą tiksliuose moksluose. Pirmasis inžinierius-fizikas, kuris teoriškai ir eksperimentiškai nustatė radijo ryšio galimybes buvo H. Hercas. Todėl dažnio matavimo vienetas pavadintas jo vardu. Manau, kad naudinga žinoti H. Herco požiūrį į matematiką. Jis rašė: „kartais atsiranda jausmas, kad matematinėms formulėms būdinga savarankiškas gyvenimas su savu protu, kad jos protingesnės už mus, netgi protingesnės už tuos, kurie sukūrė jas, kad jos duoda daugiau, negu į jas buvo įdėta“.
Garsus matematikas akademikas A. Andronovas, tvirtina, kad „sistemų tiesiškumas yra išimtinai retai pasitaikantis, unikalus atvejis“. Įsiklausius į šio garsaus pasaulyje mokslininko frazę, tiesiog negali atsistebėti, kodėl iki šiol beveik visi aukštosios matematikos pagrindai universitetuose skirti „ištiesintiems“ matematiniams modeliams. Gal būt todėl, kad tai jau yra klasika, kuri buvo kuriama kelis šimtmečius. Naudojant matematinius modelius praktiniuose inžineriniuose skaičiavimuose (bent jau elektronikoje), visada jaučiamas „ištiesintų“ matematinių modelių ribotos galimybės, kadangi yra visa eilė atvejų, kada „ištiesinti“ matematiniai modeliai neatspindi visos eilės praktikoje fiksuojamų reiškinių (pavyzdžiui, difuzinių procesų modeliai). Ypač tai tapo aišku, kada pradėjo formuotis katastrofų teorija, kadangi čia jokia „ištiesinta“ teorija negali paaiškinti tai, kas vyksta praktikoje ir kas įvardinama, kaip katastrofos.
Kaip žinia, funkcijos gali būti apibrėžiamos diferencialine lygtimi, geometrine interpretacija arba eilute. Jeigu sin ir cos apibrėžimui naudoti diferencialinę lyti, tai ši lygtis bus tiesinė. Neosinusai – sph ir cph apibrėžiami netiesine diferencialine lygtimi, todėl galima laikyti, kad tai bendresnis atvejis. Čia paminėtina Donaldo Zanevičiaus knyga „h – geometrija. Neosinusų naudojimas skaičiavimams“, kurios pirmame tome rašoma tik apie vieną neosinusų grupę – sph ir cph. Kitame knygos tome bus parodyta kita neosinusų grupė, į kurią įeina funkcijos gph (geometrinės progresijos funkcija), shpx ir chpx (sinus ir kosinus hiperbolinės-parabolinės funkcijos), kuriomis galima naudotis, kai dėl kai kurių priežasčių netinka klasikinės funkcijos exp, shx ir chx.
Neosinusų panaudojimas, formuojant sistemų lygtis, leidžia gauti algebrines lygtis, kurios daugelyje atveju gali būti išspręstos analitiškai. Kampo dydžiai matuojami radianais ir parametras h yra surišti griežta matematine priklausomybe. Tokius dydžius vadinsime identiškais. Sinα ir sph dydžiai pilnai sutampa, jeigu α ir h dydžiai yra identiški. Todėl, visa eile atveju, atsiranda galimybė analitiškai išspręsti trigonometrines lygtis ar net trigonometrinių lygčių sistemas. Įrodoma, kad trigonometrinėse lygtyse sinα pakeitus sph, kur h yra identiškas α (tai galioja ir kitoms trigonometrijos funkcijoms) vietoje trigonometrinės (transcendentinės) lygties gausime algebrinę lygtį, kuri visą eilę atveju gali būti išspręsta analitiškai. Tai, be abejo, palengvintu visos eilės praktinių uždavinių sprendimą. Pateiksime pavyzdį.
V. Paliūno vadovėlyje, skirtame universitetų mechanikos specialybės studentams (Teorinė mechanika. Vilnius Mokslas 1982 m.), yra pavyzdys 5.1. Ant gelžbetoninės plokštės prikabinami trys lynai A, B, C. Laisvi trijų lynų galai sujungiami į vieną mazgą, už kurio kabinamas krano kablys. Duodami gelžbetoninės plokštės linijiniai gabaritai a, b, d ir svoris P. Reikia suskaičiuoti jėgas, kurios veikia lynus. Pasinaudojus pusiausvyros sąlygomis, gaunamos lynus veikiančių jėgų išraiškos. Pateisime vieną iš jų:
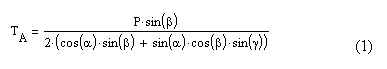
Čia pateikiamas konkretus pavyzdys:
Toliau skaičiavimo procedūra maždaug tokia. Pradžioje suskaičiuojami kampai α, β, γ. Įdomu tai, kad nei uždavinio formavimo pradžioje, nei pateikiant skaičiavimo rezultatus kampo sąvokų nėra. Kampus reikia įsivesti tik tam, kad norint gauti jėgos vektoriaus projekciją į koordinačių ašis, naudojamasi vektorinėje algebroje priimtomis kampo trigonometrijos funkcijomis sin, cos, tg. Tai šimtmetinė vektorinės algebros ir kompleksinių skaičių teorijos tradicija. Iš pateiktos formulės (1) gaunama:

Kiti pavyzdžiai pateikti minėtame teorinės mechanikos vadovėlyje rodo, kad dauguma atveju lygtys, kuriose yra transcendentinės funkcijos sin,cos tg tiesiogiai nesisprendžia ir lieka vienintelis būdas tokias lygtis išspręsti – iteracijų būdas. Reikia pasakyti, kad ir kitose technikos mokslo šakose, kuriose plačiai naudojamos kampo trigonometrijos apskritime – transcendentinės funkcijos sin, cos, tg, taip pat susiduriama su tuo, kad lygtys, kuriose yra transcendentinės funkcijos gali būti išspręstos tik iteracijų būdu.
Jeigu aukščiau pateiktą uždavinį spręsti neosinusų pagalba, tai vietoje (1) gausime:
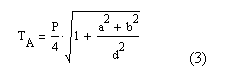
Įstatę į (3) a, b, d, P reikšmes gausime tokį pat atsakymą (2), kaip ir naudodamiesi išraiška (1), kur pradžioje reikia pasirašyti formules, kad surasti kampus α, β, γ, vėliau suskaičiuoti sin ir cos tam panaudojus begalines eilutes ir tik po to gausime atsakymą. Kaip matome iš čia pateikto vienintelio pavyzdžio, nauda pereiti prie neosinusų matematinių modelių akivaizdi.
Knygoje „h – geometrija. Neosinusų naudojimas skaičiavimams“ parodoma, kaip atrodo lygtys aprašančios elipsę. Elipsė yra viena iš labai populiarių geometrinių figūrų, kurios randa platų pritaikymą įvairiose mokslo ir technikos srityse: tai ir geodezija ir įvairūs mechanizmai. Mechanizmų teorijoje neosinusų panaudojimo prasmė parodyta sudarant alkūninio mechanizmo modelį. Aerodinamikoje ir hidromechanikoje vienas iš esminių klausimų yra sparno teorija. Knygoje parodoma kaip neosinusų pagrindu sukurtas modelis leidžia skaičiuoti sparno parametrus.
Tolimesni tyrimai parodė, kad neosinusų, vietoje sin ir cos, panaudojimas kompleksinių skaičių teorijoje ir vektorinėje algebroje duoda įdomių rezultatų.
O apie likusias funkcijas iš neosinusų šeimos gph, shpx ir chpx ir jų panaudojimą įvairiose mokslo ir technikos srityse (elektronikoje ir t. t.) galėsite rasti Donaldo Zanevičiaus knygos „h – geometrija. Neosinusų naudojimas skaičiavimams“ antrame tome.
