Įžanga
Tikiu, kad daug kas esate pajutę tą jausmą, kai norisi sukonstruoti kažką įdomaus. Mano atvejis ne išimtis, todėl panorau paprasto, nelabai brangaus ir su pavyzdžiais internete projektėlio, kurio esmė būtų ne geležies konstravimas, bet programavimas, kas labai aktualu kai neturi savo dirbtuvėlių. Labiausiai man patikusi tema buvo ant dviejų ratų kaip riedžiai balansuojantys robotai. Projekto pradžioje mokėjau tik pamirgsenti LED'ą su „Atmega8“ mikrovaldikliu ar pasukioti žingsninį motorą. Sukonstravus balansuojantį robotą prikaupiau nemažai šio roboto konstravimui reikalingos informacijos, todėl nusprendžiau ja pasidalinti. Tikiuosi pateikta informacija bus naudinga. Sėkmės!
1. Kas tas balansuojantis robotas?
 1 pav. |
|---|
Balansuojantis robotas (angl. self balancing robot) internete standartiškai yar pateikiamas kaip stačiakampis gretasienis karkasas su dviem ratukais apačioje (pav. 1), jis laikosi vertikaliai nenuvirsdamas, važinėjasi, sukiojasi į šonus, tai daro pagal komandas arba savarankiškai.
Tokio roboto esmė ta, kad jis sukiodamas ratukus pirmyn arba atgal išlaiko pusiausvyrą. Nesu tikras dėl vertimo, tačiau fizikine prasme šio roboto veikimas pagrįstas „invertuota švytuokle“, ang. „inverted pendulum“.
Radau nemažai pavyzdžių internete, kur remiantis invertuota švytuokle sudarinėjamas roboto fizikinis modelis ir pagal jį kuriamas pats robotas bei jo valdymas. Tačiau čia jau aukštasis pilotažas ir paprastam robotui tokiam kokį surinkau aš, fizikinio ar kitokio modelio nereikia.
Paprastų žmonių kalba tokio roboto balansavimas reiškia ne ką kitą, o procesą kai paimi šluotą, apverti ją aukštyn kojom ir uždėjęs ant delno slankioji ranką į šonus, kad šluota nenuvirstų. Remdamasis tokia idėja veikia ir dviem ratais balansuojantis robotas – ratai sukiojami pirmyn arba atgal, kad robotas nenuvirstų, tačiau yra vienas supaprastinimas, kad roboto nereikia balansuoti į šonus kaip šluotos, lygsvara laikoma tik pirmyn arba atgal.
Nors iš pirmo žvilgsnio pažiūrėjus vaizdelius internete apie balansuojančius robotus arba matant gyvai, pavyzdžiui, riedį atrodo, kad jie tik stovi, tačiau iš tikro tokie žaisliukai vienu metu atlieka nemažai užduočių, pagrindinės jų yra:
- Kontroliuoja savo posvyrio kampą (balansuoja).
- Kontroliuoja savo masės centro judėjimo greitį žemės atžvilgiu (greičio valdymas).
- Kontroliuoja savo poziciją.
- Daug kitų sistemų apsaugai nuo nuvirtimo, nuotolinis valdymas ir kiti dalykai.
 |
|---|
Pats primityviausias balansuojančio roboto variantas sugeba tik balansuoti ir nenuvirsti. Toks robotas nelabai kur pritaikomas, nes viskas, ką sugeba – tik stengiasi nenuvirsti. Tai problema, nes nėra sekamas judėjimo greitis ir, pavyzdžiui, stumtelėjus robotą į šoną, jis pradeda greitėti, o valdymo algoritmas į į tai nereaguoja, nes jo užduotis – tiesiog neleisti robotui nuvirsti. Kol viskas vyksta variklių sukimosi greičio diapazone – viskas gerai, tačiau kai robotas pradeda judėti greičiau nei sugeba suktis motorai – BUM... Todėl privertus robotą nevirsti, reikia realizuoti greičio valdymą, vėliau pozicijos valdymą, taip pat apgalvoti kaip robotas turi elgtis nuvirtęs ir panašiai. Tačiau vien tik balansuojantis robotas yra pirmas rezultatas, kurį reikia pasiekti norint sukonstruoti rimtesnį robotą.
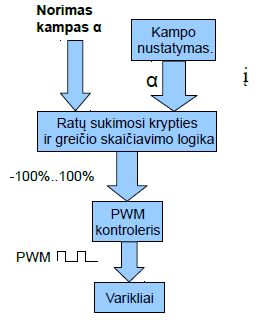
Pateiktoje schemutėjė yra nubraižyta kokiu principu robotui organizuojamas balansavimo valdymas. Viskas pradedama nuo to, kad reikia žinoti kokį posvyrio kampą norima palaikyti. Tik balansuojant užduodamas kampas yra pastovus ir lygus = 0° (valdant ir greitį užduodamas kampas yra keičiamas). Po to reikia pamatuoti kiek robotas yra pasviręs žemės atžvilgiu iš tikro. Žinant šias reikšmes yra paskaičiuojama kiek ir į kurią pusę reikia sukti ratus. Jie gali būti sukami tarkim -100 %..0..100 % variklių greičio diapazone. Šitas greitis yra nurodomas variklių valdikliui, o šis jau valdo ratų motorus.
Populiariausias būdas valdyti motorus, kurį naudojau ir aš yra DC variklių valdymas PWM būdu. Šioje schemutėje parodytos valdymo sistemos dalys detaliau aprašysiu toliau, dabar tik paminėsiu, kad roboto posvyrio kampas nustatomas prietaisėliais „MEMS akselerometru“ ir „MEMS giroskopu“ po to jų parodymai apdorojami mikrovaldiklyje, o ratus pagal paskaičiuotą reikšmę suka variklių valdiklis, realizuotas dalinai mikrovaldiklyje, dalinai mikroschemoje L298.
Kad pradėtume konstruoti vien tik balansuojantį robotą, reikia paeiliui išsiaiškinti šiuos dalykus:
- Suprasti kaip veikia balansavimas.
- Išmokti gauti „korektišką“ posvyrio kampo reikšmę.
- Suprasti kaip veikia PID reguliatorius ir kaip juo kontroliuoti balansavimą.
Atlikus šiuos namų darbus galima pereiti prie „geležies“, o iki to pabandysiu atsakyti į visus šiuos klausimus iš eilės.
Pusiausvyros laikymas
 2 pav. |
|---|
Balansuojančio roboto konstrukcijų gali būti įvairių, bet kaip minėjau, dažniausiai tai yra stačiakampio gretasienio formos karkasas su apačioje pritvirtintais dviem ratukais.
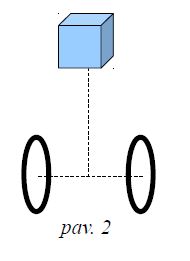
Nesvarbu koks korpusas, bet esminiai dalykai lieka tie patys, vienoje ašyje yra du ratukai, o virš tos ašies yra roboto masės centras kaip eskize dešinėj (2 pav.). Svarbiausi parametrai, nusakantys skirtingus robotus, yra ratų skersmuo, atstumas tarp ratų, masės centro atstumas nuo ašies, roboto masė.
Mąstant dar paprasčiau, jeigu į tokį skeletą kaip nupiešiau pasižiūrėti iš šono, kad matytųsi tik vienas ratas tuomet bus matomas toks vaizdas kaip piešinėlyje apačioje (pav. 3).
Robotą dabar galime įsivaizduoti kaip strypelį (pieštuką) su ratuku apačioje ir svareliu viršuje (koks 10 kg. :) ) ir kuris gali judėti tik plokštumoje pirmyn (eskize dešinėn) arba atgal (eskize kairėn). Pagal brėžinuką roboto viršuje yra jo masės centras, kurį sunkio jėga visą laiką traukia prie žemės. Stovėdamas vertikaliai robotas yra pusiausvyros taške.
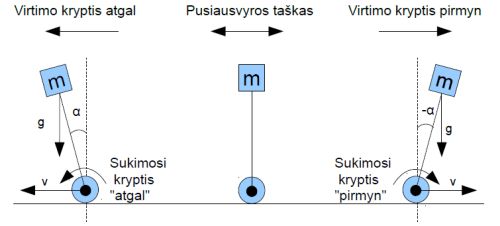
3 pav.
Jam bent truputį pakrypus nuo pusiausvyros taško jis pradeda svirti ta kryptimi, kuria pajudėjo, pirmyn arba atgal. Balansavimo prasme robotas turi tris būsenas:
- Virsta atgal.
- Pusiausvyros taškas.
- Virsta pirmyn.
Kad ir kaip bandyti robotą pastatyti rankomis į pusiausvyros tašką, jei ratai nėra kvadratiniai, to vistiek nepavyks padaryti ir robotas visvien virs į vieną, ar kitą pusę. Normaliai dirbdamas robotas visą laiką truputį svyruoja, nors gerai suderintame robote kartais to ir nesimato. Kad išlaikyti robotą vertikaliai, ratukai sukiojami pirmyn arba atgal, priklausomai nuo pavirtimo kampo „α“. Pasakymas „suktis pirmyn“ arba „atgal“ yra susitarimo reikalas, tačiau omenyje turiu, kad sukdamiesi pirmyn ratai stumia roboto apačią į priekį (eskize į dešinę), sukdamiesi atgal – stumia roboto apačią atgal (eskize į kairę). Roboto masės centras yra viršuje, todėl apatinė dalis yra lengvesnė nei viršus ir gali judėti greičiau. Taigi, jeigu robotas virsta atgal, ratai taip pat sukasi atgal bei stumia roboto apačią virtimo kryptimi. Apačia paveja viršų, robotas išsitiesina ir persvyra į priekį.
Dabar jau robotas pasviręs į priekį, vadinasi ratukai taip pat pradeda suktis į priekį stengdamiesi ištiesinti robotą. Po kurio laiko robotas vėl persvyra atgal ir šis procesas vyksta nepertraukiamai. Panašiai kaip ir su aukštyn kojomis apversta šluota kaip minėjau anksčiau, delnas yra stumdomas į tą pusę į kurią virsta šluota, kaip ir robotas važiuoja į tą pusę į kurią jis virsta, kad išlaikyti pusiausvyrą.
Sulėtinti roboto virtimą galima dviem būdais, pakeliant jo masės centrą aukščiau arba didinant roboto masę, tai yra inertiškumą. Pirmasis mano roboto korpusas buvo tiesiog pailga organinio stiklo plokštelė su pritvirtinta prie jos elektronika ir apačioje prisukti varikliai su ratais. Bet kadangi robotas buvo labai lengvas ir gana žemas aš nesugebėjau priversti jo balansuoti ir nenuvirsti. Kai pagaminau ganėtinai masyvų ir aukštą korpusą (koks 0,3 kg ir 30 cm) ir sumontavau bateriją viršuje, beveik iš pirmo karto robotas pradėjo rodyti kažką panašaus į balansavimą.
Roboto posvyrio kampo nustatymas
Net ir sąlyginai maži elektroniniai įrenginiai (telefonai, žaidimų pulteliai ir panašiai) sugeba nustatyti savo pakrypimą žemės atžvilgiu. Tai yra padaroma dviem mažais elektroniniais prietaisėliais – MEMS akselerometru ir MEMS giroskopu. „MEMS“ reiškia mikromechaninės elektroninės sistemos. Užrašymas „MEMS“ nusako, kad tai ne pusę stalo užimantys iš fizikos pamokų žinomi prietaisai, o mikroschemose sumontuotos mikromechaninės sistemos. Paėmus į rankas tai yra tiesiog mažytės kelis kvadratinius milimetrus užimančios mikroschemėlės. Plačiau apie šių prietaisėlių veikimą galite paskaityti internete įvedę „MEMS Accelerometer“ arba „MEMS Gyroscope“, o aš pamėginsiu aprašyti šiuos du prietaisėlius jų matuojamo fizikinio dydžio ir gražinamos reikšmės prasme, bei kaip iš turimų parodymų gauti „kokybišką“ roboto posvyrio kampo reikšmę. Kad būtų paprasčiau, toliau šiuos prietaisus vadinsiu tiesiog akselerometru ir giroskopu.
Akselerometras
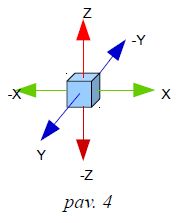 4 pav. |
|---|
Jau pats pavadinimas sako, kad jis matuoja akseleraciją – pagreitį. Matuojamas yra linijinis pagreitis, tas pats pagreitis kurį pajunti kai autobusas pradeda stabdyti, kai sėdi automobilyje, o jis greitėja ar stoja. Tačiau svarbiausiai, kad akselerometras gali išmatuoti žemės laisvojo kritimo pagreitį g savo ašių atžvilgiu, robotui tai aktualu nes galime nustatyti kuria kryptimi yra grindys. Visi kuriuos nagrinėjau akselerometrai matuoja akseleraciją trimis ašimis X,Y,Z, kaip paveikslėlyje šone (pav. 4). Kuri ašis kuri yra susitarimo reikalas, bet gamintojai aprašymuose nurodo kuri kryptis mikroschemoje atitinka kurią ašį. Viduje akselerometrai turi krūvelę registrų, tai registrai skirti saugoti matavimų reikšmes, būsenos registrai, konfigūraciniai registrai.
Tarkime turite ar planuojate nusipirkti akselerometrą, nuo ko pradėti? Toliau reikia žinoti kokioje skalėje akselerometras matuoja ir kaip gražina reikšmę. Vieni akseleromerai gražina reikšmę analoginio signalo pavidalu, kiti naudojant kokią nors komunikaciją, mano projektėlyje akselerometro (LSM303DLHC) reikšmė yra gražinama per I2C magistralę, todėl toliau aprašysiu kaip naudoti tokio tipo akselerometrą, nes jį geriausiai žinau. Pirmiausiai tiems, kas nesate susidūrę su I2C reikėtų pastudijuoti šią magistralę. Kai I2C ryšys veikia ir galima nuskaityti vidinius akselerometro registrus, jį dar reikia sukonfigūruoti (matavimo skalė, dažnis… ).
Konfigūravimas tai tiesiog tam tikrų reikšmių įrašymas į akselerometro konfigūravimo registrus, kaip pavyzdžiui konfigūruojant laikmatį mikrovaldiklyje. Kas ir į kurį registrą turi būti įrašyta paaiškinta akselerometro „datascheet'e“. Svarbiausi parametrai yra matavimo jautrumas ir duomenų atnaujinimo dažnis. Jautrumu yra nurodoma kokį didžiausią pagreitį sugeba išmatuoti akselerometras. Akselerometro matavimo reikšmės taip pat saugomos registruose. Mano akselerometro parodymų duomenys vienai ašiai yra patalpinti į du 8 bitų registrus, dvi dedamąsias „L“ (angl. low) ir „H“ (angl. High). Nesu tikras kaip reikėtų lietuviškai vadinti baitų „L“ ir „H“ skirstymą, bet L vadinsiu „mažesnioji“ dedamoji, „H“ „didesnioji“ dedamoji. Pavyzdžiui ašiai „X“ akselerometre duomenys saugomi registruose pavadinimais „OUT_X_L_A“ ir „OUT_X_H_A“, analogiškai dar keturi likusioms ašims. Pilna akseleracijos reikšmė yra dviejų baitų kombinacija ir užima 16 bitų. „C“ kalbje dviejų baitų sujungimas į 16 bitų reikšmę aprašomas pavyzdžiui taip:
X_akseleracija = (uint16_t)OUT_X_H_A <<8 | OUT_X_L_A;
Sukuriamas kintamasis kuriame bus saugoma akseleracijos reikšmė ir jai priskiriami sukombinuoti į krūvą registrų „OUT_X_L_A“ ir „OUT_X_H_A“ duomenys (gaunama reikšmė vadinama angl. „RAW data“). Taigi tarkim pavyko nuskaityti ir gauti vertę „0x0000 – 0xFFFF“ diapazone, kas toliau? Toliau RAW duomenis tiesiog interpretuojant kaip paprastą integer tipo kintamąjį su ženklu gaunama reikšmė diapazone −32767...0...+32767.
X_akseleracija = (int16_t)((uint16_t)OUT_X_H_A <<8 | OUT_X_L_A);
Akselerometras gali būti sukonfigūruotas dirbti jautrumu +/-2g, +/-4g, +/-8g, +/-16g („g“ ne gramai, o laisvojo kritimo pagreitis!). Kad pamatyti tikrąją g reikšmę reikia gautus parodymus padauginti ar padalinti iš koeficiento, kuris nusako jautrumą. Mano atveju esant jautrumui +/-2g reikia gautąją reikšmę padalinti iš 16384. Programoje registro dedamųjų sujungimą ir perskaičiavimą į realų fizikinį dydį „g“ galima užrašyti taip:
X_akseleracija = ((int16_t)((uint16_t)OUT_X_H_A <<8 | OUT_X_L_A))/16384;
Kadangi mano mikrovaldiklis turi slankiojo kablelio modulį aš skaičiuoju taip:
X_akseleracija = ((float)((int16_t)((uint16_t)OUT_X_H_A <<8 | OUT_X_L_A)))
/16384.0f;
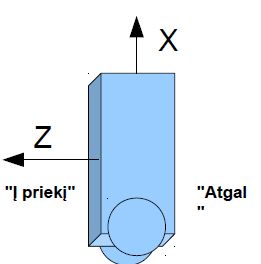 5 pav. |
|---|
Parodymų patikrinimas paprastas, kaip žinome iš fizikos laisvojo kritimo pagreičio reikšmė yra 1g, taigi jei viskas gerai, akselerometras nejudinamas nukreipus kurią nors jo ašį į žemę pamatuos 1g arba -1g reikšmę toj ašy. Dėl krūvos priežasčių bent jau paprastų akselerometrų parodymai ko gero visada yra su paklaidom. Jas galima, bet nėra būtina programiškai koreguoti. Reikia tiesiog pasiekti, kad būtų rodoma tarkim -1g ir +1g reikšmės nukreipiant akselerometro ašį statmenai į žemę arba į dangų. Norint, kad kampas būtų skaičiuojamas teisingai yra svarbu, kad tos ašys iš kurių parodymų bus skaičiuojamas posvyrio kampas rodytų kuo vienodesnes reikšmes kai jos paeiliui yra nukreiptos į žemę arba į dangų.
Kai jau žinomi visų ašių parodymai galima pereiti prie pavirtimo kampo skaičiavimo. Skaičiavimams reikalinga vertikali ir horizontali ašis kaip parodžiau piešinėlyje greta (pav. 5). Mano robote sumontavus PCB su akselerometru į korpusą vertikalia ir horizontalia tapo akselerometro Z ir X ašys. Kampas yra skaičiuojamas iš Z ir X ašių akseleracijos reikšmių. Jeigu jūsų akselerometras atsistotų kitaip, galima kurią nors reikšmę imti su minuso ženklu, imti kitokias ašių kombinacijas, rezultatas turi būti toks, kad vertikaliai stovinčio roboto paskaičiuotas posvyrio kampas būtų lygus nuliui ir kai robotas pavirtęs į tą pusę kurią vadinate „į priekį“ kampas būtų neigiamas. Kampas skaičiuojamas pagal formulę:
Kampas=(atan(Z_akseleracija/X_akseleracija))*57.2957f;
57.2957 yra reikalinga perskaičiuojant reikšmę iš radianų į laipsnius. Plačiau internete apie kampo skaičiavimą iš akselerometro parodymų galima rasti įvedus paieškoj frazę „accelerometer tilt angle calculation“.
Apibendrinant, kad gauti kampą pasitelkus akselerometrą, reikia:
- Išmokti gauti duomenis iš akselerometro.
- Nuskaityti akseleracijų reikšmių duomenų registrus.
- Sulipdyti duomenis į reikšmes ašims X, Y, Z, kad gauti taip vadinamus „RAW“ duomenis.
- Perskaičiuoti gautąsias reikšmes į realią fizikinę prasmę turinčias reikšmes.
- Priklausomai nuo akselerometro orientacijos iš dviejų reikšmių (vertikalios ir horizontalios kaip parodžiau aukščiau) paskaičiuoti pasvirimo kampą.
Giroskopas
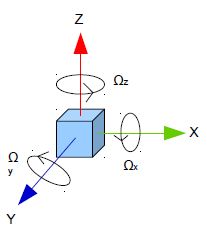 6 pav. |
|---|
Kaip ir akselerometras, giroskopas reikalingas nustatyti roboto posvyrio kampą, tačiau skirtumas tarp jų yra tas, kad giroskopu matuojame ne linijinį pagreitį, bet kampinį greitį (Ω), kaip pavaizduota piešinėlyje 6. Kaip ir akselerometras giroskopas viduje turi krūvelę registrų kuriais yra konfigūruojamas ir kuriuose talpina matavimų rezultatus. Duomenų paėmimui iš giroskopo taip pat yra keletas būdų. Gali būti I2C, SPI interfeisas, analoginis signalas. Mano robote yra naudojamas „L3GD20“ giroskopas, kuris pajungtas per SPI interfeisą („cool“ interfeisas mano nuomone). Duomenų registrai sudėlioti analogiškai akseleromerui. Po dvi dedamąsias kiekvienai ašiai, viso šeši registrai. Pavyzdžiui „X“ ašiai „OUT_X_L“ mažesnioji reikšmės dedamoji, „OUT_X_H“ didesnioji dedamoji. Visus šešis duomenų registrus taip pat reikia sujungti į krūvą, kad rezultate būtų trys registrai po 16 bitų.
Dedamųjų sujungimas kaip ir akselerometro atveju atrodo taip:
X_kampGreitis_tmp = OUT_X_H <<8 | OUT_X_L;
Taigi situacija kartojasi, turite tris reikšmes diapazone nuo 0x0000 iki 0xFFFF, ką daryti toliau? Toliau sudėtingesnė dalis kuri man sekėsi sunkiau, nes neatidžiai skaičiau giroskopo aprašymą, atsakymą radau tik skaitydamas forumus. Žodžiu griroskopas kaip ir akselerometras yra konfigūruojamas, vieni iš svarbiausių parametrų yra duomenų atnaujinimo dažnis, jautrumas. Su duomenų atnaujinimo dažniu ko gero klausimų nekilo, bet jautrumas sudėtingesnis dalykas. Giroskopo jautrumas nusakomas laipsniais per sekundę (angl. DPS- degrees per second). Mano giroskopas gali būti konfigūruojams 250/500/2000 DPS jautumu. Kuo didesnis jautrumas, tuo mažesnę kampinio greičio reikšmę matuoja giroskopas.
Giroskopo duomenų išraiška laipsniais per sekundę yra gaunama „RAW“ duomenis konvertuojant į žėnklą turintį kintamąjį (manu buvo patogu „float“) ir padauginant iš jautrumą nusakančio koeficiento, kuris yra duodamas giroskopo aprašyme. Mano atveju prie 2000 DPS koeficientas yra 0,07. Kad gauti „float“ tipo giroskopo parodymus, programoje duomenų sujungimas ir konvertavimas iš „RAW“ atrodo taip:
X_kampGreitis= ((float)((int16_t)((uint16_t)OUT_X_H <<8 | OUT_X_L)))*0.07.0f;
Nuo čia pusė darbo jau atlikta, bet kampo reikšmės dar neturime. Jeigu kalbėtume apie linijinį greit, tai būdas iš linijinio greičio gauti poziciją yra greičio integravimas, su kampiniu greičių tas pat tik kampui gauti integruojamas kampinis greitis. Gal ir skamba sudėtingai, bet iš tikro integravimas atliekamas labai paprastai, rekia susikurti kintamąjį tarkim „kampas“ kuris ir yra paskaičiuota kampo reikšmė ir kaskart gavus naujus duomenis „kampas“ kintamajam priskirti save patį plius nauji duomenys padauginti iš laiko intervalo (T) per kurį tie duomenys buvo gauti.
„kampas = kampas + X_kampGreitis * T“
Žinant, kad periodas (T) ir dažnis (f) yra vienas kitam atvirkščiai proporcingi dydžiai, galima perrašyti šitą taip:
„kampas = kampas + X_kampGreitis / f“
Man tai pasirodė patogiau, nes mano atveju kai duomenų nuskaitymo dažnis 760 Hz nereikia imti periodo reikšmės 1/760 Hz=0,001315..473.. be galo be krašto.…, pakanka naudoti skaičių 760, taigi aš skaičiuoju galutinę kampo reikšmę ašiai X taip:
kampas = kampas + X_kampGreitis / 760;
Ir dabar jau turime konkrečią kampo reikšmę!
Apibendrinant, kad gautume kampą giroskopu, reikia:
- Išmokti gauti duomenis iš giroskopo.
- Nuskaityti duomenų registrus.
- Sukombinuoti 8 bitų registrų reikšmes į 16 bitų.
- Perskaičiuoti reikšmes į prasme turinčius dydžius laipsniais/s
- Suintegruoti gautus duomenis kiekvienai ašiai atskirai, kad gauti kampą.
Akselerometru ir giroskopu gautų reikšmių kombinavimas
Turėjote užduoti sau klausimą, kodėl reikalingas ir akselerometras, ir giroskopas jei iš jų abiejų galima gauti kampo reikšmę? Atsakymas toks: ir akselerometras ir giroskopas dirbdami pavieniui turi „kritinių“ trūkumų kampo skaičiavimui.
Kuo blogas akselerometras?
Jis skaičiuoja kampą pagal laisvojo kritimo pagreičio vektoriaus projekcijas akselerometro X, Y, Z ašyse.
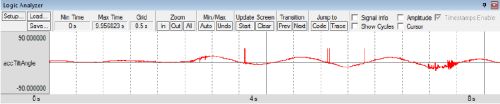
Taščiau gali atsirasti ir kitas pagreitis. Akselerometras nežino pagreičio prigimties, tiesiog pagal išmatuotas reikšmes ašyse paskaičiuoja koks būtų pokrypio kampas stacionarioje būsenoje. Paprastai kalbant – gauna sprigtą ir pašėlsta. Kadangi turiu galimybe atvaizduoti vidinius mikrovaldiklio kintamuosius, paveikslėlyje apačioje parodžiau kaip kinta iš akselerometro parodymų apskaičiuota roboto posvyrio kampo reikšmė, robotą palengva judinat į šonus (motorai atjungti).
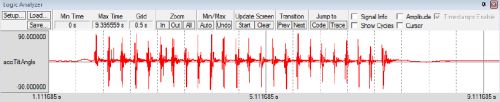
O sekančiame paveikslėlyje matote, kas būna kai robotas visai nėra judinamas, bet kumščiu stuksenu jam per viršų. Nors jo posvyrio kampas beveik nesikeičia, bet jis sugeba išmatuoti net kokį 80° posvyrio kampą. Tai ir yra negerumas, kadangi veikdamas robotas ir kratosi ir dreba ir taip toliau, todėl kampo reikšmės paskaičiuotos tik iš akselerometro duomenų naudoti negalima. Kai kurie žmones naudoja signalo filtrus, bet kiek žiūrėjau internete vaizdo įrašų su tokiais robotais, tai rezultatas „robotas drebalas“, tačiau iš bėdos įmanoma.
Kuo blogas giroskopas?
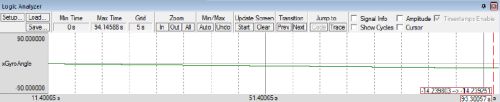
Tuo, kad kampo skaičiavimui naudoja integravimą, o MEMS giroskopo parodymai nėra idealūs, tai reiškia kad prisumavus bet kokią klaidingą reikšmę ji lieka bendrame rezultate, integruojasi į bendrą rezultatą. Idealių reikšmių gauti vistiek nepavyks, net ir ramiai gulintis robotas rodo palengva kintantį kampą, nor jis ramiai guli. Kaip matote, atlikus kampo registravimą, jau po 93 sekundžių kampas nuo 0° pasikeitė iki 14,23°, su tokia kampo paklaida robotas tikrai neveiks. O blogiausiai, kad šitas kampo svyravimas labai priklauso nuo temperatūros. Deja mano naudojamas giroskopas forumuose labai kritikuojamas dėl didelių triukšmų ir signalo poslinkio. Todėl planuoju ateityje pažaisti su kitokiais giroskopais.
Beja, neapsigaukite kai sakau, jog matavau kampą robotui gulint, o matavimai prasideda nuo 0°, kai turėtų būti apie 90° su vienu ar kitu ženklu. Viskas tvarkoje, tiesiog kai mikrovaldiklis startuoja ir nėra kampo korekcijos (kurią tuoj aprašysiu), integravimas prasideda nuo pradinės reikšmės, pas mane ji „0“. nesvarbu kaip paguldysiu robotą, startuodamas jis vistiek pradės skaičiuoti nuo nulio.
Kaip išvengti akselerometro ir giroskopo trūkumų?
Gana paprastai. Nesu tikras kaip tai vadinama lietuviškai, jei neklystu komplementariniu filtru, bet internete šis metodas vadinamas angl. „sensor fusion“. Jo esmė yra ta, kad giroskopas atsparus vibracijoms, tačiau jis integruoja paklaidą, akselerometras paklaidos neintegruoja, tačiau yra jautrus vibracijoms. Bet sukombinavus šių dviejų prietaisų parodymus, galima akselerometru kompensuoti giroskopo kaupiamą paklaidą. Tai yra daroma labai paprastai, tiesiog giroskopo reikšmė periodiškai perskaičiuojama paimant tarkim 99,9 % giroskopo reikšmės ir 0,1 % akselerometro reikšmės, ir rezultatą vel suteikiant giroskopo reikšmei (gali būti ir kitoks santykis). Pas mane programoje tai įgyvendinta šitaip:
giroKampas = giroKampas * 0.999f + akselKampas * 0.001f;
Labai svarbu kad koeficientų prie akselerometro ir giroskopo reikšmių suma būtų lygi 1 (pvz. 0,999 ir 0,001), nes kitaip rezultato pasiekti nepavyks, ilgai vargau kol supratau kur bėda, kai šitoje vietoje padariau klaidelę.
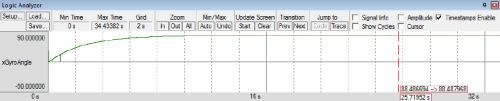
Kaip matote iš matavimų pateikų žemiau, su kampo korekcija net ir imant 0,001 akseleromrto reikšmės ir įjungus robotą kai jis paguldytas giroskopo reikšmė yra ištaisoma į tikrąją. Giroskopas pradėjo skaičiuoti nuo nulio, bet po maždaug 8 sekundžių akselerometras atstatė giroskopo reikšmę į 480 (tikroji reikšmė). Mažinant santikį tarp koeficientų akselerometras greičiau koreguoja giroskopo reikšmę, tačiau didėja giroskopo jautrumas vibracijoms.
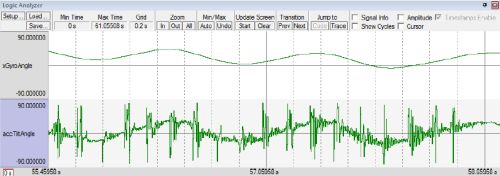
Žemiau pateikti matavimai konkrečiai atspindi kokį rezultatą duoda signalų kombinavimas. Čia xGyroAngle yra giroskopu skaičiuojamas kampas jau su korekcija, accTiltAngle tik akselerometru skaičiuojamas kampas.
Tuo metu kai registravau kampo reikšmes robotas buvo judinamas į šonus ir tuo pat metu kumščiu stuksenau per viršų. Galite palyginti kaip smarkiai skiriasi rezultatai.
Taip pat reikia turėti omenyje, kad skaičiuojant kampą akseleromeru yra naudojama dalyba, pradiniu momentu kai visi kintamieji yra lygūs nuliui kaip tik ir vykdoma dalyba iš nulio. Vėlia kitose iteracijose viskas atsitaiso, bet bėda kita. Nežinau kokia reikšmė mikrokontroleryje gaunama dalinant iš nulio, bet po to kai panaudojamas komplementarinis filtras tai yra suintegruojama į bendrą kampo rezultatą ir mikrokontroleris užsikeikia, kampo skaičiavimas nevyksta. Todėl reikia realizuoti apsaugą nuo dalybos iš nulio, tiesiog tais atvejais kai akselerometro ašių parodymai lygūs nuliui, priskirti jiems pavyzdžiui 0,000001 reikšmę.
Labai svarbu:
- Koeficientų prie akselerometro ir giriskopo reikšmių suma turi būti lygi vienetui!
- Kampų paskaičiuotu akselerometru ir giroskopu atskirai ženklai privalo būti vienodi!
- Apsauga nuo dalybos iš nulio skaičiuojant kampą akselerometru!
PID reguliatorius
Žinant kokiu būdu robotas laiko pusiausvyrą, tai yra, kad virsdamas į pirekį pavažiuoja į priekį, o virsdamas atgal pavažiuoja atgal, žinant kaip nustatomas tikrasis roboto posvyrio kampas žemės atžvilgiu, lieka klausimas kaip pagal turimą kampo reikšmę paskaičiuoti kiek gi iš tikro pasukti ratukus viena ar kita kryptim. Atsakymas yra – reguliatorius, jis žino kiek pasukti ratukus.
Pats vienas reguliatorius neturi prasmės, jis naudingas tik tuomet, kai yra valdymo sistemos dalis. Kokios būna valdymo sistemos, kaip jos veikia nagrinėja automatinio reguliavimo (arba valdymo) teorija. Tai „didelis“ mokslas tačiau konstruojant robotą pakanka tik suprasti esmę kaip veikai schemos su grįžtamuoju ryšiu, kaip veikia PID reguliatorius tokiose schemose. Valdymo sistemos prasmė yra tokia, kad priklausomai nuo to kas valdoma, valdymo sistemai užduodama norima gauti proceso reikšmė (pozicija, greitis, temperatūra ar kt.), o ji savarankiškai užtikrina, kad tai būtų pasiekta. Valdymo su gržtamuoju ryšiu sitemoje turi būti kažkas, ką reikia valdyti ir kažkas, kas valdo. Tai ką valdome yra vadinama „Valdymo objektu“. Valdymo objektas roboto atveju yra korpusas su baterija, ratukais, varikliais ir variklių valdikliu. Tai sistema, kuriai nurodai į kurią pusę ir kaip smarkiai sukti ratukus, o ji priklausomai nuo savo parametrų sureaguoja, tai yra pasvyra į vieną, ar kitą pusę. Valdymo objektą galima atvaizduoti grafiškai (pav. 12). Rodyklė kairėje vaizduoja poveikį valdymo objektui, o rodyklė dešinėje jo reakciją į poveikį.

12 pav.
Valdymo objektų yra visokių, visi jie skirtingai reaguoja į valdymo poveikį. Matematiškai valdymo objektas yra aprašomas perdavimo funkcija. Tačiau dažniausiai, kaip ir roboto atveju nebūtina žinoti kokia yra objekto perdavimo funkcija. Konstruojant robotą pakanka turėti omeny, kad vien tik balansuojančio roboto atveju valdymo objektas yra mano minėta sistema, kuriai perduodi skaičiką kiek ir į kurią pusę sukti ratukus, o ji priklausomai nuo savo savybių sureaguoja – pasikeičia roboto posvyrio kampas kurį mes pamatuojame kaip sistemos išėjimą. Va čia ir paaiškėja kam reikalingas reguliatorius – jis yra ta valdymo sistemos dalis, kuri žino kiek ir į kurią pusę sukti ratukus, kad robotas laikytų užduotą kampą. Paveiksle pav. 13 pavaizduota pati paprasčiausia valdymo schema su grįžtamuoju ryšiu.
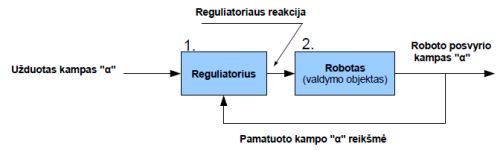
13 pav.
Vien tik balansuojančio roboto atveju šią sistemą galime suprasti taip: Turime robotą (valdymo objektą), jis pažymėtas „2.“ kvadratėliu schemoje. Reguliatorius „1“ grįžtamuoju ryšiu paima tikrąją roboto posvyrio kampo reikšmę, taip pat užsiduoto kampo, kurį norime palaikyti reikšmę, palygina jas ir priklausomai nuo to, kiek jos skiriasi, ratukų valdikliui nurodo pasisukti į vieną ar kitą pusę, kad tikrasis kampas kiek galima labiau priartėtų prie užsiduoto. Po tam tikro laiko reguliatorius vėl „pasižiūri“ kaip pakito roboto kampas ir pasuka ratukus. Šitaip procesas vyksta nepertraukiamai kol veikia robotas. Priklausomai nuo valdymo objekto, grįžtamasis ryšys gali būti neigiamas arba teigiamas. Dažniausiai yra naudojamas neigiamas grįžtamasis ryšys. Šitoje schemutėje yra vienas paprastas valdymo kontūras su vienu reguliatoriumi, vienu valdymo objektu, vienu grįžtamuoju ryšiu, tačiau sistemos būna ir kaskadinės, kur yra keli kontūrai apimantys vienas kitą, keli grįžtamieji ryšiai. Automatikoje procesų valdymui yra naudojama visokių reguliatorių P, PI, PD, PID ir kitokių, tačiau populiariausias yra PID reguliatorius. Valdymo sistemos su PID reguliatoriumi eskizas pateiktas žemiau. Kai kurie žymėjimai nesutaps su pateikiamais literatūroje, nes noriu pateikti viską kuo paprasčiau.
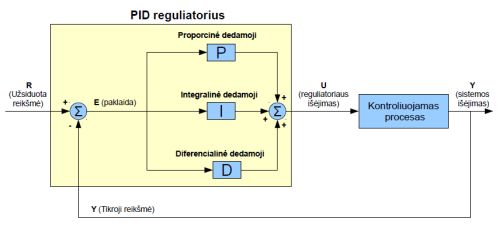
Pavadinimas P.I.D yra duotas todėl, kad reguliatorius skaičiuoja koks bus jo išėjimas iš trijų dedamųjų: Proporcinės, Integralinės ir Diferencialinės. Pateiktoje schemoje reguliatorius apima dalį gelsvame fone. Kaip matote iš schemutės paprastas PID reguliatorius turi du įėjimus ir vieną išėjimą. Pirmasis įėjimas yra ta reikšmė kurią norime palaikyti – nuostatas „R“ (angl. setpoint), kitas įėjimas grįžtamasis ryšys (angl. feedback), tai yra tikroji valdomo objekto išėjimo reikšmė „Y“ (roboto atveju tikrasis pavirtimo kampas).
Reguliatorius skaičiavimus pradeda nuo įėjimo reikšmių palyginimo. Tam, kad žinoti kiek šios reikšmės skiriaisi tarpusavyje naudojamas palyginimo elementas „Σ“ arba kitaip sumatorius. Jis pagal ženkliukus prie rodykliu sudeda arba atima tarpusavy jam paduodamas reikšmes. Palyginimo elemetas reguliatoriaus įėjime atima iš norimos reikšmės tikrają reikšmę (pvz. norimas kampas minus tikrasis kampas), matematiškai tai užrašomas taip E = R – Y. Užsiduotos ir esamos valdymo reikšmių skirtumas yra vadinamas paklaida „E“ (angl. error). Toliau atsižvelgiant į gautą paklaidą atskirai yra skaičiuojamos reguliatoriaus proporcinė, integralinė ir diferencialinė dedamosios. Kai šios dedamosios yra paskaičiuotos, jos visos sudedamos sumatoriaus pagalba, o rezultatas yra PID reguliatoriaus išėjimas: U= P + I + D. Taigi, trumpas apibendrinimas – paskaičiuojamas skirtumas norima reikšmė minus tikroji reikšmė (paklaida), pagal šitą skirtumą atskirai paskaičiuojamos P, I ir D dedamosios, jų reikšmės sudedamos, o rezultatas yra PID reguliatoriaus išėjimas – paprasta.
Sumuojant skirtingas dedamųjų kombinacijas gaunami skirtingi reguliatoriai: P, PI, PD, PID. Egzistuoja daugybė objektų kuriuos galime valdyti reguliatoriaus pagalba ir konkrečios objektų savybės nulemia ar pasirinktas P, PI, PD, PID reguliatorius išvis gali suvaldyti sistemą ir jei taip kaip kokybiškai jis tą padaro. Galima būtų labai išsiplėsi aprašinėjant kaip skirtingi reguliatoriai susitvarko su skirtingo pobūdžio valdomomis sistemomis, tačiau paminėsiu tik tai, kas reikalinga balansuojančio roboto valdymui. Taigi kaip žinoti ar reguliatorius susitvarko su roboto balansavimu be grafikų ar kokių nors skaičiavimų? Paprastai, jei robotas nenuvirsta, vadinasi reguliatorius jau susitvarko, o pagal tai kaip robotas švytuoja, drebą, reaguoja į trikdį (stumtelėjimą) matosi kaip reguliatoriui sekasi susitvarkyti. Kiek kokybiškai turi balansuoti robotas yra kiekvieno skonio reikalas. Man svarbu kad robotas vizualiai nedrebėtų, nešvytuotų ir atsitiesintų stumtelėjus jį tarkim 7° į šoną.
Parenkant reguliatorių balansavimui pasakysiu, kad iš tikro tai vien balansavimui beveik pakanka ir P reguliatoriaus, bet tuomet robotas būna labai nestabilus, nenuvirsti sugeba gana trumpai, išvedi iš pusiausvyros labai nedaug, jis įsibėgėja į tą pusę kur stumtelėjai ir bum... Tuomet galima bandyti PI reguliatorių, kuris pilnai susitvarko su balansavimo užduotimi. PID reguliatorius žinoma dar geriau, bet jį sudėtingiau ir suderinti, o kadangi mano robote yra keletas valdymo kontūrų: ratų sukimosi greičio, masės centro judėjimo greičio, balansavimo, tai ėmiau kiek galima paprastesnes reguliatorių išraiškas, kad lengviau viską suderinčiau, tačiau apie kitus kontūrus dabar neišsiplėsiu. Beja visai įdomus užsiėmimas bandyti visokias dedamųjų kombinacijas ir matyti kaip skirtingai jos dirba ir kaip elgiasi robotas. O dabar apie dedamąsias.
Proporcinė dedamoji
Proporcinė dedamoji parodo kiek reguliatoriaus išėjimas proporcingas paklaidai. Proporcinę dedamąją skaičiuoti paprasčiausia. Tarkim, reikia palaikyti 0° pavirtimo kampą, o robotas pavirtęs į priekį, reguliatorius grįžtamuoju ryšiu gauna tikrąją posvyrio kampo reikšmę pavyzdžiui -5°, palyginimo elementas jas palygina ir gauname E= 0° - (-5°), arba tiesiog E= 0 + 5 = 5. Kadangi dedamoji vadinama „proporcinė“ tai galima užrašyti P = U (P – proporcinė dedamoji). Roboto atveju jau galime PWM kontroleriui užduoti 5 % reikšmę sukti ratukus pirmyn. Bet ar tiek pakanka? Gal reikia sukti ratukus smarkiau? O galbūt 5 % per daug?
Va nuo šios vietos atsiranda labai svarbus vienas iš trijų reguliatoriaus derinimo parametrų stiprinimo koeficientas „Kp“. Jis parodo kiek stipriai proporcinė dedamoji reaguoja į paklaidą. Dabar proporcinė dedamoji atrodo šitaip: P = E * Kp. Kokio dydžio reikia šito koeficiento priklauso nuo daug sąlygų, jo nustatymas vadinamas reguliatoriaus derinimu. Pid reguliatoriaus atveju yra viso trys koeficientai. Dabar skaičiuojant su praktiniu pavyzdžiui kai paklaida vis dar 5, o stiprinimo koeficientas buvo nustatytas tarkim 8, pagal formulę P = E * Kp gauname: P= 5*8= 40, vadinasi PWM = 40 %. Ir kaskart suskaičiavus naują paklaidos reikšmę reguliatorius persiskaičiuoja ir proporcinę dedamąją:
- E = -1 tai PWM = -1 * 8 = -8; Ratukis sukti atgal ir PWM= 8.
- E = 2 tai PWM = 2 * 8 =16; Ratukis sukti pirmyn ir PWM= 16.
- E = -3 tai PWM = -3 * 8 =-24; Ratukis sukti atgal ir PWM= -24.
Šitaip reguliatorius skaičiuoja nepertraukiamai. Turint tik proporcinę dedamąją jau galime tokį reguliatorių dernti. Jo derinimas yra paprastas, reikia didinti Kp reikšmę kol prasideda svyravymai (pradeda drebėti), po to truputį sumažinti. Didinant Kp robotas greičiau, aršiau reaguoja į paklaidą, tačiau sistemoje atsiranda svyravimai. Žinant kaip skaičiuojama P dedamoji jau galima pradėti lipdyti PID reguliatorių programoje. Savo robotui reguliatorių parašiau kaip funkciją, kurią gali naudoti kiek tik nori kartų, kuriai perduodi tik nuostato reikšmę, grįžtamojo ryšio reikšmę, struktūrą su reguliatoriaus parametrais ir kitais kintamaisiais, o reguliatorius gražina paskaičiuotą reikšmę kaip paprasta funkcija. Funkcijos pseudo kodas atrodo taip:
...
float PID(nuostatas , grįžtamasis_ryšys , parametrai){
„P“ dedamosios skaičiavimas;
...
„I“ dedamosios skaičiavimas;
...
„D“ dedamosios skaičiavimas;
...
PIP_išėjimas = P + I + D;
return PIP_išėjimas;
}
…
Pradedant programuoiti veikiantį PID reguliatorių kurio veikimą testuosite jau reikia turėti kintamuosius su tikrojo posvyrio kampo reikšme, reikia turėti veikiantį PWM valdymą, tarkim šie kintamieji atrodo taip:
...
float kampas; //Kintamasis, kuriame saugoma tikroji kampo reikšmė.
flota PWM; //PWM reikšmė variklių valdikliui.
...
Toliau aprašomas struktūros tipo kintamasis reguliatoriaus parametrams. Nor dar ne visus parametrus aprašiau, bet parametrų struktūra atrodo taip:
…
/* parametrų struktūros aprašas */
struct parameters{
float Kp; //Stiprinimo koeficientas
float Ki; //Integravimo koeficientas
float Kd; //Diferenciavimo koeficientas
float Integral; //Kintamasis paklaidos integralui saugoti
float Prev_error; //Kint. paklaidos reikšmei iš ankstesnės iteracijos
};
...
Sukuriamas struktūros tipo kintamasis, kurį reikia perduoti į funkciją (reguliatorių):
...
struct parameters balancingParam; //Sukuriamas „parameters“ tipo
kintamasis.
...
Priskiriamos reguliatoriaus parametrų reikšmės pradedant nuo Kp:
balancingParam.Kp = 100; //Kp reikšmė
/* Kiti parametrai, kuriuos neužilgo aprašysiu*/
Toliau galima lipdyti patį reguliatorių. Pagal anksčiau pateiktą pseudo kodą reikia susikurti funkciją, kuriai perduodama nuostato reikšmė, grįžtamojo ryšio reikšmė, struktūra su parametrais ir kintamasis kuris norodo kokiu dažniu atliekami reguliatoriaus skaičiavimai (vykdoma funkcija), jis bus aktualus kitų dedamųjų skaičiavimui. Kintamuosius vadinau anglų kalba, bet visus žodžius paaiškinau jau anksčiau. Taigi:
...
float PID(float freq /* vykd. Dažnis */, float setpoint, float feedback,
struct parameters *par){
/* Vidiniai funkcijos kintamieji */
float PIDOutput; // Kintamasis, kurį reguliatorius grąžins.
float error; // Paklaidos reikšmė.
float P_term; // Proporcinė dedamoji.
/* Paklaidos skaičiavimas */
error = setpoint – feedback; //Paklaidos skaičiavimas.
/* P dedamosios skaičiavimas */
P_term = error * par-> Kp; // Proporcinės dedamosios skaičiavimas
/* I dedamosios skaičiavimas */
/* D dedamosios skaičiavimas */
/* išėjimo skaičiavimas (P + I + D) */
PIDOutput = P;
/* Reikšmės grąžinimas */
return PIDOutput;
}
...
Jeigu šitaip aprašytumėte PID reguliatorių programoje, jis jau pilnai veiktų kaip „P“ reguliatorius, o praktinis panaudojimas atrodo pavyzdžiui taip:
PWM = PID(760 , 0 , kampas , &balancingParam);
Ir viskas! Viena eilutė ir naudoji reguliatorių. Tačiau kaip ir minėjau balansavimui tik proporcinio reguliatoriaus nepakanka, reikalingas bent PI reguliatorius.
Integralinė dedamoji
Kas tai yra ir ką daro integralinė dedamoji? Jau aišku, kad proporcinis reguliatorius dirba ne visai kaip norėtųsi. Taip yra todėl, kad balansavimas yra inertiška sistema ir, kad ją suvaldyti reguliatoriui reikia žinoti ne tik kaip sistema elgiasi duotuoju laiko momentu, bet ir anksčiau. Reguliatorius turi turėt „atmintį“ apie tai kaip sistema reaguoja. Tą būtent ir atlieka integralinė dedamoji. Viena iš blogybių kuo P reguliatorius negeras, yra statinė paklaida. Lengviausiai ją suprasti būtų nagrinėjant tarkim temperatūros palaikymą. Pavyzdžiui reikia palaikyti 100° temperatūrą katile, tačiau jis praranda šilumą ir sugeba įšilti tik iki 95° laipsnių. Reguliatorius pamatuoja esamą temperatūrą ir pagal ją paskaičiuoja kiek kaitinti katilą. Tačiau niekaip nepasiekia užsiduotos temperatūros nes nežino, kad katilas vėsta, kad šitaip kaitinti jau bandė bet rezultato nepasiekė. Todėl reikia, kad reguliatorius būtų su atmintim ir dirbtų maždaug taip:
- Iteracija 1: Pamatavau temperatųrą, ji per žema 5° tai pakaitinu katilą.
- Iteracija 2: Pamatavau temperatųrą, ji per žema 5°, pakaitinu katilą smarkiau.
- Iteracija 3: Pamatavau temperatųrą, ji per žema 5°, pakaitinu katilą dar smarkiau.
Analogiškai ir su robotu, tik čia dar įdomaiu. Vien su P reguliatoriumi balansavimas veikia taip: Beveik ties 0° robotas galima sakyti balansuoja ir kurį laiką nenuvirsta, tačiau nuo mažiausio stumtelėjimo ar kliūties jis niekaip nebesugeba grįžtį į 0°, nes atsiranda statinė paklaida.
Reguliatorius paskaičiuoja kiek reikėtų pasukti ratukus, kad grįžti į reikiamą kampą, bet dėl trinčių, liuftų ar panašiai nepasiekia 0°. Gaunasi taip, kad robotas pastumtas važiuoja greitėdamas į tą pusę į kurią buvo stumtelėtas, bet vis tiek neatsitiesina ir galiausiai virsta. Kp didinimas iki tam tikro lygio padeda, bet bėda neišsisprendžia, nes atsiranda smarkus drebėjimas. Šioje vietoje kaip ir su katilo šildymu reikia, kad reguliatorius žinotų, jog paskaičiuotas poveikis buvo per silpnas ir esant tokiai pačiai paklaidai kaip ir ankstesniame skaičiavime ratai būtų pasukami smarkiau. Toks efektas yra gaunamas integruojant paklaidą. Integralinė dedamoji yra suintegruota paklaida padauginta iš koeficiento (Ki). Roboto atveju ji veikia taip:
- Iteracija 1: kampas 2°, suku ratus pirmyn.
- Iteracija 2: kampas 2°, suku ratus smarkiau pirmyn.
- Iteracija 3: kampas 1,5°, suku ratus dar smarkiau pirmyn.
- Iteracija 4: kampas 1°, suku ratus dar smarkiau pirmyn.
- Iteracija 5: kampas 0,5°, suku ratus dar smarkiau pirmyn.
- Iteracija 6: kampas 0°, nebėra paklaidos, integralinė dedamoji nepadidėjo, bet ir nesumažėjo, vadinasi vis dar suka ratus pirmyn.
- Iteracija 7: kampas -0,5° , ratai dar vis sukami pirmyn, bet jau silpnai.
- Iteracija 8: kampas -1° , ratai nebesukami pirmyn, integralinė dedamoji lygi nuliui.
- Iteracija 9: kampas -1,5° , Integralinė dedamoji vėl pradeda augti tik jau su minuso ženklu.
- Ir taip procesas kartojamas nepertraukiamai...
Integralinė dedamoji be savo gerųjų savybių įneša į sistemą nestabilumą, tačiau naudojama kartu su kitomis dedamosiomis duoda reikiamą rezultatą. Integralinė dedamoji skaičiuojama taip:
Integral = Integral + error * reguliatoriaus_vykdymo_periodas;
arba:
Integral = Integral + error / reguliatoriaus_vykdymo_dažnis;
Šitokiu užrašymu kiekvienos iteracijos metu reikšmei „Integral“ yra priskiriama jos pačios reikšmė ir paklaida padauginta iš laiko, per kurį ji atsirado. Čia viskas analogiškai giroskopo reikšmės integravimui, tik integruojami ne giroskopo parodymai, o paklaida. Labai svarbus dalykas yra galimybė valdyti integralinės dedamosio indėlį į reguliatoriaus išėjimą, tam naudojamas mano minėtas koeficientas Ki. Dabar jau galime užrašyti galutinę integralinės dedamosios išraišką:
Integral = Integral + error / reguliatoriaus_vykdymo_dažnis;
I_term = Integral * Ki ;
Parametrų stuktūrai šalia Kp priskiriama ir Ki reikšmė:
balancingParam.Kp = 100; //Kp reikšmė
balancingParam.Ki = 200; //Ki reikšmė
/* Kiti parametrai, kuriuos neužilgo aprašysiu*/
Sukėlus viską į reguliatoriaus funkciją gauname:
...
float PID(float freq /* vykd. dažnis */, float setpoint, float feedback,
struct parameters *par){
/* Vidiniai funkcijos kintamieji */
float PIDOutput; // Kintamasis, kurį reguliatorius grąžins.
float error; // Paklaidos reikšmė.
float P_term; // Proporcinė dedamoji.
float I_term; // Integralinė dedamoji.
/* Paklaidos skaičiavimas */
error = setpoint – feedback; //Paklaidos skaičiavimas.
/* P dedamosios skaičiavimas */
P_term = error * par-> Kp; // Proporcinės dedamosios skaičiavimas
/* I dedamosios skaičiavimas */
par->Integral = par->Integral + error / freq;
I_term = par->Integral * Ki; // Integralinės dedamosios
skaičiavimas
/* išėjimo skaičiavimas (P + I + D) */
PIDOutput = P + I;
/* Reikšmės grąžinimas */
return PIDOutput;
}
…
D dedamoji
Ir trečioji dedamoji yar vadinama diferencialine. Jos dydis priklauso nuo paklaidos kitimo greičio per laiką, kuo greičiau keičiasi paklaida, tuo didesnė diferencialinė dedamoji, jei paklaida nesikeičia, diferencialinė dedamoji lygi nuliui. Kitaip sakant diferencialinė dedamoji proporcinga paklaidos kitimo greičiui. Matematiškai ji skaičiuojama taip:
diferencialas = (paklaida – ankstesne_paklaida) /
reguliatoriaus_vykdymo_periodas;
arba:
diferencialas = (paklaida – ankstesne_paklaida) *
reguliatoriaus_vykdymo_daznis;
O kad valdyti diferencialinės dedamosios indelį į reguliatoriaus išėjimą, įvedamas koeficientas Kd. Diferencialinės dedamosios skaičiavimui programoje pirmiausiai reikai nurodyti Kd reikšmę:
balancingParam.Kp = 100; //Kp reikšmė
balancingParam.Ki = 200; //Ki reikšmė
balancingParam.Kd = 10; //Kd reikšmė
Galutinė PID reguliatoriaus išraiška atrodo taip:
...
float PID(float freq /* vykd. dažnis */, float setpoint, float feedback,
struct parameters *par){
/* Vidiniai funkcijos kintamieji */
float PIDOutput; // Kintamasis, kurį reguliatorius grąžins.
float error; // Paklaidos reikšmė.
float P_term; // Proporcinė dedamoji.
float I_term; // Integralinė dedamoji.
float D_term; // Diferencialinė dedamoji.
float diferential; // paklaidos diferencialas.
/* Paklaidos skaičiavimas */
error = setpoint – feedback;
/* P dedamosios skaičiavimas */
P_term = error * par->Kp;
/* I dedamosios skaičiavimas */
par->Integral = par->Integral + error / freq;
I_term = par->Integral * par->Ki;
/* D dedamosios skaičiavimas */
diferential = (error - par->Prev_error) * freq;
D_term = diferential * par->Kd;
par->Prev_error := error;
/* išėjimo skaičiavimas (P + I + D) */
PIDOutput = P_term + I_term + D_term;
/* Reikšmės grąžinimas */
return PIDOutput;
}
…
Štai ir viskas, šitoks reguliatorius jau moka balansuoti robotą. Turiu paminėti, kad pas mane yra kelios kosmetinės modifikacijos apriboti ingralinę dedamąją, reguliatoriaus išėjimą bei galimybė perjungti parametrų derinius iš agresyvesnių į švelnesnius tam, kad prie didelio pavirtimo kampo robotas reaguotų aršiau, bet tai nėra būtina.
Kai robotas jau pagamintas ir turi šitokį veikiantį reguliatorių, lieka jį suderinti. Apie PID reguliatoriaus derinimą yra daugybė informacijos internete, paminėsiu tik tai, kad balansavimui derinimas galėtų būti tarkim toks:
- Pastatyti visus parametrus į 0 reikšmę.
- Didinti Kp koeficientą kol robotas pradės daugmaž balansuoti.
- Didinti Ki reikšmę kol robotas pradės pakankamai stabiliai veikti.
- Po to galima eksperimentuoti kaiteliojant reikšmes siekiant išgauti kuo stabilensį veikimą.
Info apie mano robotą
„Geležis“
Svarbiausios roboto sudedamosios dalys yra mikrovaldiklis, akselerometras, giroskopas, varikliai.
Skaitinėdamas internete kokie būna šitie daikčiukai, radau neblogą žaisliuką, bandymų plokštę, kurioje sumontuoti būtent mikrovaldiklis, akselerometras, giroskopas, krūva LED ir programatorius, skirtas plokštės programavimui per USB. Bėda buvo tik ta, kad tai ne „Atmelio“ žaislas su kokia nors „Atmega“, bet ST gaminys pavadinimu „STM32F3 DISCOVERY", kuris varomas ARM tipo mikrovaldikliu.
Jo kaina siunčiantis iš „ebay“ yra apie 25 doleriai (apie 23 eurus). Turint omeny, kad gauni paruoštą PCB ir mikrovaldiklį su slankiojo kablelio skaičiavimo moduliu + „COOL!“ USB programatorių + akselerometrą + giroskopą + LED + du mygtukus + nereikia daryti PCB + krūvą nemokamų bibliotekų, taip pat duodama tikriausiai visa įmanoma plokštės dokumentacija, todėl nusprendžiau, kad tai nėra didelė investicija, nes perkant viską atskirai, vargu ar būtų pigiau, o dar sugaištas laikas. Bet čia mano pasirinkimas. Projektuodamas robotą norėjau, kad viskas būtų kuo kompaktiškiau, todėl nusprendžiau pasidaryti dar vieną plokštę, prie kurios reikėtų jungtelėmis prijungti varikliukus, maitinimą ir kuri būtų sujungiama su „Discovery“ plokšte. Rezultatas toks:

Kaip matote, išėjo kompaktiškas įrenginukas, kuris gali kontroliuoti robotą. Mano paties suprojektuota ir kiniečių pagaminta plokštė parodyta žemiau. Dėja nepavyko išvengti kelių klaidelių, jas teko pataisyti peiliuku, vielute ir lituokliu. Tačiau rezultatas – plokštė, kuriai pajungus DC maitinimą 7..18 V ribose, prijungus varikliukus su enkoderiais bei prijungus „Discovery“ plokštę, nebereikia rūpintis elektrine dalimi, lieka tik programavimas. Kaip ir minėjau pradžioje man to būtent ir reikėjo.
Nors schemutės nebeturiu, tačiau ji labai paprasta, variklių valdymui mikroschema L298, su mikrovaldikliu sujungta per buferiuką 74HC2450, įtampos reguliatorius 7805, kelios jungtelės, rezistoriai, diodai ir kondensatoriai.
Panaudojau tipinę L298 pajungimo schemą tik modifikavau sijungimui su „Discovery“ plokšte. Kinietis pagamino viso šešias plokštes ir vienos savikaina berods apie 8 EUR.
Varikliukai DC su reduktoriumi ir enkoderiu, modelis JGA25-371-12-463RPM, vieno kaina apie 8 EUR.


Baterija paimta nuo akumuliatorinio 18 V gręžtuvo. Taip pat nepaminėjau „Bluetooth“ adapteriuko. Jam dėja nenumačiau pajungimo plokštėje, todėl pabandymui buvau tiesiog sujungęs laidukais su jungtelėmis prie „Discovery“ plokštės. Gal nuotraukose ir nesimato, bet „Discovery“ plokštė turi krūvą pin'ų viršuje ir apačioje. Korpusas paprasčiausias stačiakampis karkasas iš organinio stiklo ir kelių metalinių strypelių su sriegiu.
Roboto programavimas
Kadangi roboto konstravimas yra įdomus laiko leidimo būdas, negailėjau laiko norėdamas išmokti kažką naujo. Pramokau programuoti ARM CORTEX šeimos mikrovaldiklį STM32F303VCT6 ir realaus laiko operacinę sistemą FREERTOS, programavimui naudojau „Keil uVision5“ aplinką, iki tam tikro dydžio kompiliuojamo failo ji yra nemokama. Nebandau užsiimti reklama, tačiau kombinacija „Discovery“ plokštė + „Keil Uvision“ tikrai šaunus dalykas mokantis ARM mikrovaldiklius. Kad pradėti programuoti „Discovery“ plokštę reikia nemokamai parsisiųsti „Keil uVision“, įdiegti USB tvarkyklę „Discovery“ plokštėje esančiam „ST link“ programatoriui, projekte nustatyti, kad jis ir bus naudojamas, paprastu „USB mini B“ laidu prijungti „Discovery“ plokštę prie kompiuterio ir viskas, jau galima programuoti. Pirmiausiai pradedant nuo paruoštų pavyzdžių ir palengva modifikuojant kodą savo poreikiams. Esminiai dalykai, kodėl man patiko „Discovery“ ir „uVision“ kombinacija:
- Galima ne tik įrašyti, bet ir „debuginti“ programą.
- Galima matyti ir redaguoti visus vidinius įrangos registrus, realiai matyti, kas darosi su laikmačiais (taimeriais), UART sąsaja, kita įranga.
- Galima stebėti ir keisti globalių programos kintamųjų vertes.
- Slankiojo kablelio skaičiavimai atliekami specialiame modulyje taip, kad beveik nenukenčia procesoriaus greitis.
- Ir esminis dalykas, kad ARM procesoriai turi tokį „CoreSight“ modulį, kuris gali stebėti globalius programos kintamuosius, juos atvaizduoti grafiškai, bei loginti procesoriaus įvykius nesikišdamas į jo darbą, todėl kai atvaizduoji kintamąjį grafiškai, bent mano atveju duomeys atnaujinami net dešimčių mikrosekundžių greičiu! Tai suteikia galimybę jau veikiantį robotą prijungti USB kabeliu prie kompiuterio, derinti parametrus, bei grafiškai stebėti, kas vyksta su kintamaisiais. Minusas tik tai, kad grafiškai galima vaizduoti tik keturis kintamuosius vienu metu.
Kadangi plokštėje esantis mikrovaldiklis ARM tipo, reikėjo išmokti jį programuoti. Kas nežinote tai ARM yra mikrovaldiklio branduolys, tokį patį branduolį gali naudoti skirtingi gamintojai, o skirtinguose mikrovaldikliuose su tuo pačiu branduoliu skiriasi tik vidinė įranga „hardware“. Mano procesoriukas yra STM32F303VCT6, jo programavimas panašus kaip ir programuojant „Atmega“ valdiklius, programa rašoma C kalba (arba „Asembleriu“, kurio nemoku), kodas vykdomas „main“ funkcijoje „while“ cikle, viduje krūva „hardware“, kuris konfigūruojamas taip pat analogiškai „Atmega“ valdikliams. Viskas įskaitant GPIO, laimačius, UART'us ir kitus modulius programuojama panašiai, tik naudojami ne 8 bitų, bet 32 bitų registrai, taip pat naudojamos pertrauktys ir kiti mikrovaldikliams būdingi dalykai, skirtumas tik tas, kad „Hardware“ yra sudėtingesnis ir jo prigrūsta gerokai daugiau nei kokioje „Atmegoje“. Esminiai skirtumai yra tai, kad pavyzdžiui „Cortex“ šeimos ARM mikrovaldiklis yra 32 bitų ir yra gerokai artimesnis kompiuteriams, viduje turi visokių magistralių, kurios dirba skirtingais dažniais, tai pat procesorius startuoja mažu dažniu po to yra taktuojamas PLL'u iki maksimalaus dažnio ir visa tai kaip jam dirbti nurodoma startuojant. Paprastam vartotojui tuo rūpintis nereikia, kadangi procesorių gamintojai visada parašo „startup“ failą kurį jau paruoštą įterpi į projektą, tačiau visą tai reikia žinoti norint suprasti kaip dirba ARM mikrovaldikliai. Reikia išmokti nemažai naujų dalykų, tačiau viskas labai artima „Atmega“ mikrovaldiklių programavimui.
O dėl operacinės sistemos, tai puikiausiai galima išsiversti ir be jos, tiesiog norėjau suprasti kas tai yra operacinė sistema. Beja, tuo pat metu su ja žaisti pradėjo ir mano bičiulis, su kuriuo konsultuojuosi programavimo klausimais, todėl nusprendžiau ir aš daryti roboto valdymą su operacine sistema. Kas nežinote operacinių sistemų mikrovaldikliams, tai nereikia manyti, kad operacinė sistema kažkas tokio ypatingo, tai yra tik krūvelė prie projekto pridedamų failiukų, o rezultate turime tai, kad programa vykdoma ne viename „while(1)“ cikle, o paeiliui funkcijose, kurios vadinamos „taskais“, kurių viduje vėl yra po „while(1)“ ciklą ir tie „while“ ciklai vykdomi tik tiek, kiek reikia konkrečiai užduočiai atlikti. Po to „taskai“ yra stabdomi, kol jų vėl prireiks. Iš to gaunama tokia nauda, kad operacinė moka panaudoti tik tiek procesoriaus, kiek reikia konkrečiai užduočiai atlikti. Apie operacines sistemas apskritai ir apie pačią FREERTOS operacinę galite sužinoti gamintojo puslapyje arba paieškoj įvedę frazę „Freertos“.

 Tikiu, kad daug kas esate pajutę tą jausmą, kai norisi sukonstruoti kažką įdomaus. Mano atvejis ne išimtis, todėl
panorau paprasto, nelabai brangaus ir su pavyzdžiais internete projektėlio, kurio esmė būtų ne geležies
konstravimas, bet programavimas, kas labai aktualu kai neturi savo dirbtuvėlių. Labiausiai man patikusi tema
buvo ant dviejų ratų kaip riedžiai balansuojantys robotai.
Tikiu, kad daug kas esate pajutę tą jausmą, kai norisi sukonstruoti kažką įdomaus. Mano atvejis ne išimtis, todėl
panorau paprasto, nelabai brangaus ir su pavyzdžiais internete projektėlio, kurio esmė būtų ne geležies
konstravimas, bet programavimas, kas labai aktualu kai neturi savo dirbtuvėlių. Labiausiai man patikusi tema
buvo ant dviejų ratų kaip riedžiai balansuojantys robotai.